注意力机制如何起源的

神经网络中的注意力机制启发自人类的视觉注意力机制，能够（高分辨率地）聚焦于图像中需要重点关注的目标区域（节省大脑资源），同时（低分辨率地）感知周围的图像，然后随着时间的推移调整焦点（状态调整）。

在神经网路中，注意力机制是为了解决什么问题？

在深度学习还没流行的时候, 传统的算法早已应用了注意力机制的思想.

比如一个非线性回归问题，对于代表位置的输入变量${x_1, …, x_m}$ 和 代表位置对应的输出值${y_1, …, y_m}$, 如何预测新的$x_n$对应的输出? Baseline 就是求均值, $$\frac{1}{m} \sum_{i=1}^{m} y_i$$ 当然更好的方案(Watson, Nadaraya, 1964)是根据不同的输入$x_i$给与$y_i$不同的权重, $$y = \sum_{i=1}^{m} \alpha(x, x_i) y_i $$

这里$x$代表一个新的输入(作为query), 根据$x$和已有的位置$x_i$(作为key)进行某种运算, 得到$x_i$对应的输出$y_i$(作为value)的权重. 如果每一个权重都是一个Guassians分布, 并正则化, 则一个加权的回归预测模型就是:$$f(x) = \sum_i y_i \frac{k(x_i, x)}{\sum_j k(x_j, x)}$$

这个算法的"深度学习"版本, 就是其权重是通过优化器(如sgd)学习得来, 并且把平均运算改为加权池化(weighted pooling).

如何简单直观地理解注意力机制

虽然注意力机制一开始被应用于图像识别领域，但是后来推广到神经机器翻译(NMT)中(Seq2Seq for Machine Translation, Sutskever, Vinyals, Le ‘14). NMT也是注意力机制在NLP领域最早最成功的应用之一.

在上图中，Echt，Dicke和Kiste词被送到编码器中，并且在特殊信号（未显示）之后，解码器开始生成翻译后的句子。解码器不断生成单词，直到产生特殊的句子结尾标记(如<eos>)。也就是说解码器仅根据最后一个隐含状态$h_3$来生成序列. 假如这个句子很短, 那么效果其实是很好的.

不过对于比较长的句子, 那么这个架构的弱点就暴露无疑了.

  1. 首先, 编码器能否把句子的所有信息(语言学上的和常识等知识)都理解/捕捉到?
  2. 其次, 受限于目前的实现技术(主要是硬件), 单个隐含状态(如$h_3$这个向量)的维度大小是有限的, 而句子长度以及语言的组合情况是无限的, 单靠$h_3$自身是存储信息能力是有限的.
  3. 再者, 解码器是否有足够的解码能力从一个隐含状态中解码出所有的信息?

虽然大部分句子是相对紧凑的, 但语言有个特点, 就是一个词有可能和前面好几步之外的词有联系, 比如一些指代词用于指代文本最开头出现的名词; 语义上, 某个句子的理解, 可能依赖于前面多个句子; 当然往大了说, 要理解一篇文章或一本书, 我们通常需要理解并联系多个段落, 多个章节. 这种现象称之为语言的长距离依赖(long-term dependency), 在一般性的序列数据中, 这个现象称之为的Long-range dependence(LRD). 即使是使用了LSTM这种理论上可以克服长距离依赖问题地网络, 也无法很好的克服语言的长距离依赖问题, 究其原因, 除了LSTM自身的局限性之外, 更主要是深度学习的梯度学习方法的局限性(在梯度反向传播中, 会出现梯度消失).

在没有更好地参数学习方法替代, 以及隐含层容量有限的前提下, 注意力机制通过为各个时间步的词分配注意力, 从理论上赋予了模型回望源头任意时间步的能力. 注意力机制自身包含的参数是一般神经网络的重要补充, 而它的机能也一定程度上解决了梯度消失的问题.

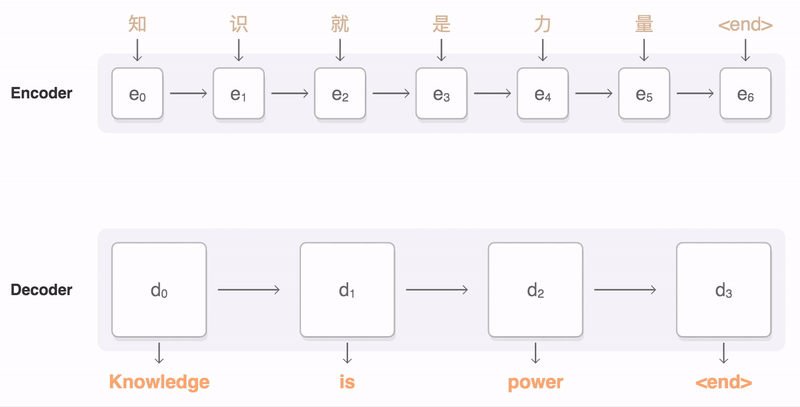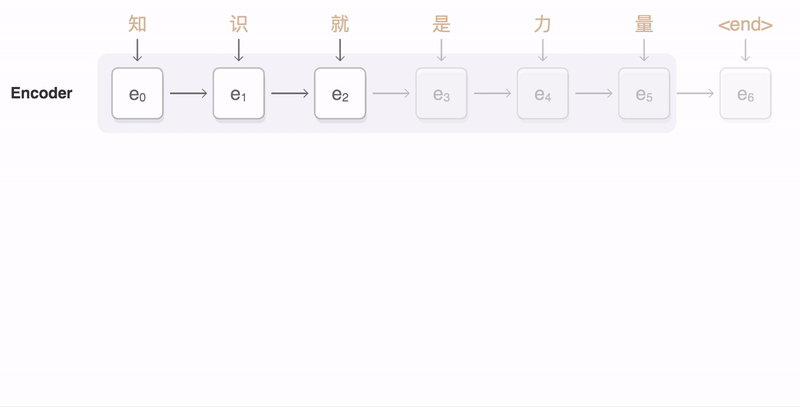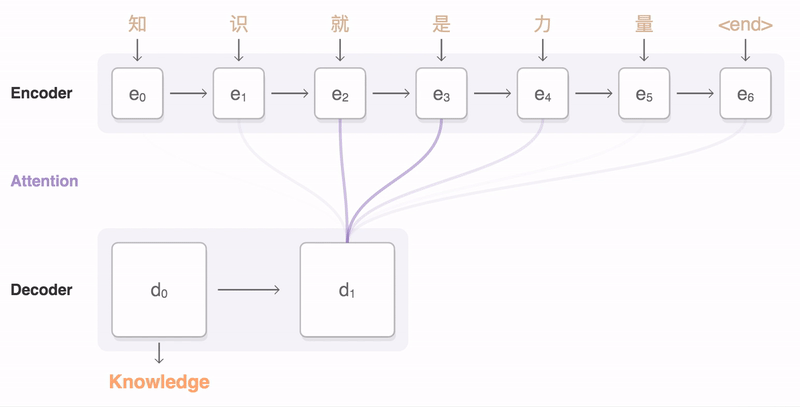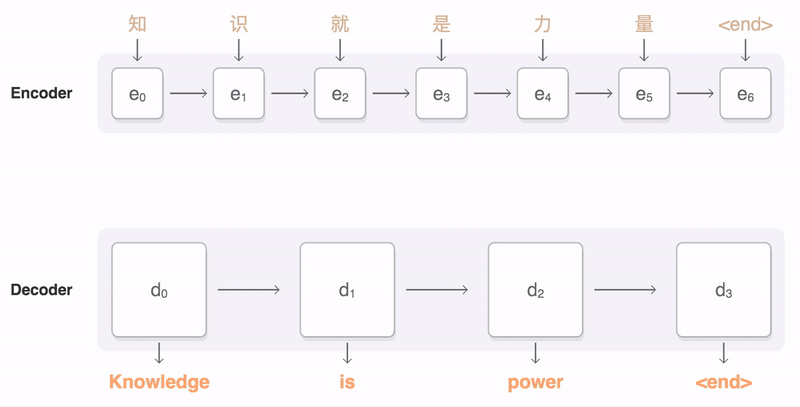
注意力机制在NMT的具体作用过程是这样, 训练过程中, 给定一对输入序列知识就是力量<end>和输出序列Knowledge is power <end>。解码器可以在输出序列的时间步1(当前时间步就是一个query), 使用集中编码了知识信息的背景变量来生成Knowledge，在时间步2使用更集中编码了就是的信息的背景变量来生成is，依此类推。这看上去就像是在解码器的每一时间步对输入序列中不同时间步编码的信息分配不同的注意力。这样注意力矩阵参数就编码了这种"注意力", 同时也更好的协助其他网络部件学习参数. 在预测阶段的每一个时间步, 注意力也参与其中.

一个经典的(目前也还在不断发展的)NLP问题是文本编码, 即把非结构化的文本, 映射为结构化的数字/向量. 较早有纯统计的Bag of words(Salton & McGill, 1986), 后期发展出了经典的Word2Vec(Mikolov et al., 2013). 现在主流的神经网络文本编码方法是Word2Vec, fasttext, rnn(lstm/gru)等, 核心思想是把文本中的每个字符都映射到一个embedding向量空间中, 全部加在一起得到整个文本的向量表示, $f(x)=\rho \bigg( \sum_{i=1}^n \phi(x_i) \bigg)$, 再拿去给后续的网络做分类等任务. 这种算法的缺陷是, 最终编码出来的向量, 会偏向统计频率高的元素, 这导致其在很多实际应用中表现不好, 比如情感分析中, 很多转折句, 前后态度是反转的, 但核心是转折后的部分.

They respect you, they really do, but you have to… Why are you laughing?

如何让编码模型重点关注句子的关键部分呢? 这得分情况, 一种如这样 They respect you, they really do, but you have to... Why are you laughing?, 整个句子的意思, 是着重于but后面的部分. 亦或者如Wang et al, ’16中提到的“The appetizers are ok, but the service is slow.”, 一个句子中其实分为两个意思, 对于外观口味，评价为积极，而对于服务，评价为消极。

那么这个时候就需要用注意力机制来给句子的编码分配权重了, $$f(x)=\rho \bigg( \sum_{i=1}^{n} \alpha(w_i, X) \phi(x_i) \bigg)$$ 通过注意力机制，我们不再需要竭尽全力把完整的句子输入编码为固定长度的向量，二十允许解码器在输出生成的每个步骤中“关注”源语句的不同部分。

所以 Attention 在神经网络模型中的作用就是改进池化(pooling): 没有Attention的池化:$$f(X)=\rho \bigg( \sum_{x \in X} \phi(x) \bigg)$$ 有Attention后: $$f(X)=\rho \bigg( \sum_{x \in X} \alpha(x, w) \phi(x) \bigg)$$

如何表达注意力机制

把Attention机制从encoder-decoder架构中抽象出来理解, 如下图: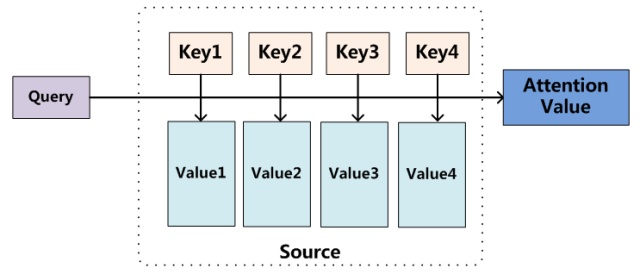

注意力三个核心组件是:

  1. Query: decoder当前待解码的输出. 如果是seq2seq模型, 那就是当前解码器待生成的时间步(用前一时间步的解码器隐含状态来表达).
  2. Key-Value: 每个key(输入序列经过编码后的隐含状态)都对应一个value. 在文本任务中, 一般Key和Value一样, 都是输入序列的编码。
  3. Query和Key的相关性: $\alpha(q, k)$, 告诉模型如何根据Query和各个Key的相关性来分配权重.

计算注意力的主要步骤:

  1. 计算Query和每个key之间的相关性$\alpha_c(q,k_i)$, 常用的相关性函数包括点积(Scaled Dot-Product Attention)，拼接，神经网路等
  2. 归一化(如softmax)后获得分配权重${\theta_1, …, \theta_k}$
  3. 计算Value的加权平均值, 作为Attention输出值.

$$\begin{eqnarray} A(q, {(k,v)}) \xrightarrow[\text{output}]{\text{maps as}} \sum_{i=1}^k{\overbrace{\alpha_c(q,k_i)}^{\theta_i}}v_i, q \in Q, k \in K, v \in V \end{eqnarray}$$

在编码器-解码器架构中，Query通常是解码器的隐含状态。而Key和Value，都是编码器的隐含状态。加权求和作为输出: $$\begin{eqnarray} out = \sum_{i=1}^k \theta_i v_i = \sum_{i=1}^k \theta_i h(x_i) \end{eqnarray}$$

Attention和Memory对比

从上面的描述看Attention更像是对神经网络(如LSTM等)的记忆功能的改进. 也就是说, 注意力机制只是让网络能够访问其内存，比如编码器的隐含状态. 网络选择从内存中检索什么，并给与不同程度的“关注度”. 换句话说, 何种内存访问机制是soft的，网络将检索所有内存并加权组合。使soft的内存访问好处是可以使用反向传播轻松地进行端对端网络训练（当然也有其他办法-采样方法来计算梯度）。

而另一方面, 更复杂的Memory机制的研究也发展地如火如荼。比如End-To-End Memory Networks(Sainbayar 2015)中提到的网络结构, 允许网络在输出之前多次读取相同的输入序列，并在每个步骤中更新内存。可以应用于, 例如通过对输入故事进行多个推理步骤来回答问题。 Joe went to the kitchen. Fred went to the kitchen. Joe picked up the milk. Joe travelled to the office. Joe left the milk. Joe went to the bathroom.

Where is the milk?

此时, 当网络参数以某种方式绑定在一起时，这个内存结构就和上面介绍的注意力机制一样了，只是它在内存上进行了多次跃迁（因为它试图集成来自多个句子的信息）。

在这种情境下, 注意力机制也可以很灵活地应用, 比如分别在字符级使用注意力机制来编码单词, 在单词级上编码句子, 在句子级上编码段落, 即 Hierarchical attention.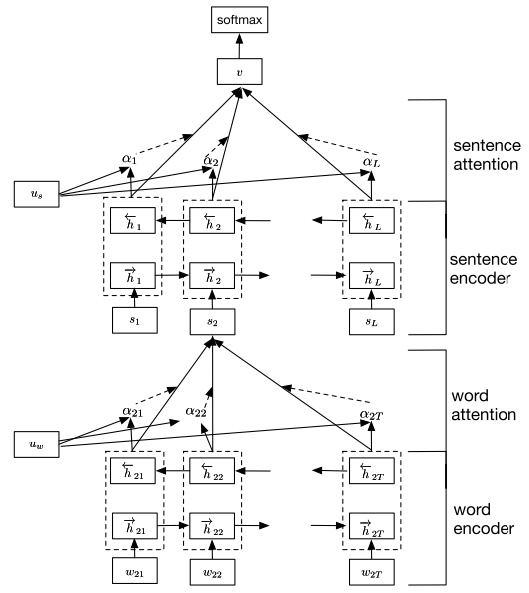

Neural Turing Machines(Graves et al., ‘14)的思想也是在内存机制上, 通过将神经网络和外部存储资源耦合来扩展神经网络的功能，这些资源可以通过注意力机制与之交互。组合后的系统类似于图灵机或冯·诺依曼架构，具有端到端的可微分性(因此可以通过梯度下降来进行训练)。除此之外, 神经图灵机但具有更复杂的寻址类型，既可以使用基于内容的寻址（如上下文），也可以使用基于位置的寻址，从而使网络可以学习寻址模式以执行简单的计算机程序，例如排序算法。

这里并不是要给出Attention和Memory机制的确切的定义区别(也给不了, 有的人觉得二者就是一个东西, 比如有人就称Attention其实软寻址, 应该称为Soft Attention), 而是从主流角度给出类比和解读.

实战案例: 注意力机制应用到机器翻译中

还是以机器翻译为例: 对于解码器的每一个时间步$t’$, 生成一个背景向量$c_{t’}$来捕捉相关的解码器信息, 以用于预测输出目标值$y_{t’}$. 解码器在时间步 $t’$ 的隐藏状态 $$s_{t’} = g(y_{t’-1}, c_{t’}, s_{t’-1}).$$ 令编码器在时间 $t$ 的隐藏状态为 $h_t$，且总时间步数为 $T$。解码器在时间步 $t’$ 的背景变量为 $$c_{t’} = \sum_{t=1}^T A{t’ t} h_t,$$ 其中 $A{t’ t}$ 是注意力分配的权重，用于给定解码器的当前隐藏状态 $s_{t’}$，对编码器中不同时间步的隐藏状态$h_t$求加权平均。$$A{t’ t} = align(s_{t’}, h_t) = \frac{\exp(score(t’ t))}{ \sum_{t=1}^T \exp(score(t’ t)) },$$ 其中 $score(t’ t) \in \mathbb{R}$ 的计算为 $$score(t’ t) = \alpha(s_{t’ - 1}, h_t).$$

上式中的score打分函数 $score(t’ t)$ 有多种设计方法。Bahanau 等使用了MLP感知机：

$$e_{t’t} = v^\top \tanh(W_s s_{t’ - 1} + W_h h_t),$$

其中 $v$、$W_s$、$W_h$ 以及编码器与解码器中的各个权重和偏差都是模型参数。

Bahanau 等在编码器和解码器中分别使用了门控循环单元GRU。在解码器中，我们需要对门控循环单元的设计稍作修改。解码器在 $t’ $ 时间步的隐藏状态为

$$s_{t’} = z_{t’} \odot s_{t’-1} + (1 - z_{t’}) \odot \tilde{s}_{t’},$$

其中的重置门、更新门和候选隐含状态分别为

$$ \begin{aligned} r_{t’} &= \sigma(W_{yr} y_{t’-1} + W_{sr} s_{t’ - 1} + W_{cr} c_{t’} + b_r), \\ z_{t’} &= \sigma(W_{yz} y_{t’-1} + W_{sz} s_{t’ - 1} + W_{cz} c_{t’} + b_z),\\ \tilde{s_{t’}} &= \text{tanh}(W_{ys} y_{t’-1} + W_{ss} (s_{t’ - 1} \odot r_{t’}) + W_{cs} c_{t’} + b_s). \end{aligned} $$

然后，给定目标(解码器)隐藏状态$h_{t’}$, 以及背景向量$c_{t’}$, 通过使用简单的并联层合并这两个向量的信息, 来生成所谓的注意力隐藏状态:

$$\tilde{h_{t’}} = \tanh(W_c[c_{t’} : h_{t’}]) $$

这个注意力向量 $\tilde{h_t}$ 之后会通过一个softmax层来生成预测的概率分布.

延伸阅读:全局注意力机制

Effective Approaches to Attention-based Neural Machine Translation(Luong et al. 2015)对应用于NMT的注意力机制进行了一定的总结：分为全局（global）和局部（local）注意力机制。区别在于“注意力”是放在所有源位置或仅放置在少数源位置。

The idea of a global attentional model is to consider all the hidden states of the encoder when deriving the context vector $c_t$.

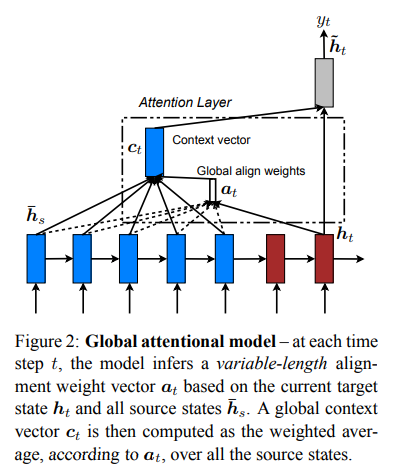两种注意力机制区别就在于如何生成背景向量$c_{t’}$.

Luong et al. (2015) 给出了几种打分函数的计算

$$ \begin{aligned} score_{dot}(t’ t) &= s^\top_{t’}h_t \\ score_{general}(t’ t) &= s^\top_{t’} W_\alpha h_t, \\ score_{concat}(t’ t) &= v^\top_\alpha \tanh (W_\alpha[s_{t’} : h_t]) \end{aligned} $$

参考资料

  1. Dzmitry Bahdanau, Kyunghyun Cho, and Yoshua Bengio. 2014. Neural machine translation by jointly learning to align and translate. arXiv preprint arXiv:1409.0473
  2. Wang, Yequan, Minlie Huang, and Li Zhao. “Attention-based LSTM for aspect-level sentiment classification.” Proceedings of the 2016 conference on empirical methods in natural language processing. 2016.
  3. Yang, Zichao, et al. “Hierarchical attention networks for document classification.” Proceedings of the 2016 Conference of the North American Chapter of the Association for Computational Linguistics: Human Language Technologies. 2016.
  4. http://www.wildml.com/2016/01/attention-and-memory-in-deep-learning-and-nlp/
  5. 目前主流的attention方法都有哪些？ - 张俊林的回答 - 知乎 https://www.zhihu.com/question/68482809/answer/264632289
  6. https://mchromiak.github.io/articles/2017/Sep/01/Primer-NN/#attention-basis
  7. Attention in Deep Learning, Elex Smola, ICML 2019, Long Beach, CA