不使用加减符号求和整数
不能使用+和-, 仅通过^和&操作来求和两个整数a.
参考
每位相加可能会产生进位(carry), 所以可以把相加拆分为两部分, 如759 + 674可以拆分为不考虑进位的部分323和仅考虑进位的部分1110, 故759 + 674 = 323 + 1110 = 1433.
二进制的加法也是从低位开始逐步往高位计算:
- 进行一位二进制的加法, 也就是暂不考虑进位的位相加:
0+0=0, 0+1=1, 1+0=1, 1+1=0, 那么就是^操作. 所得的和作为新的a. - 求进位: 通过
a & b判断是否进位, 因为只有两个位均为1才会进位. 所得的进位左移一位作为新的b. - 不断重复这个过程, 把低位的进位传递到高位, 累加到
a中, 直到进位为0, 最后得到的a就是答案.
public class Solution {
public int getSum(int a, int b) {
while (b != 0) { // 关键在于判断终止的时机
int c = a & b; //carry
a ^= b; //add
b = c << 1;
}
return a;
}
}
涉及的运算就是一个多位二进制加法真值表:(对应于硬件中的全加器)
全加器(full adder)将两个一位二进制数相加,并根据接收到的低位进位信号,输出和、进位输出。全加器的三个输入信号为两个加数A、B和低位进位Cin。全加器通常可以通过级联(cascade)的方式,构成多位(如8位、16位、32位)二进制数加法器的基本部分。全加器的输出和半加器类似,包括向高位的进位信号Cout和本位的和信号S,相加结果的总和表达为 ${\displaystyle \mathrm {sum} =2\times C_{out}+S}$。
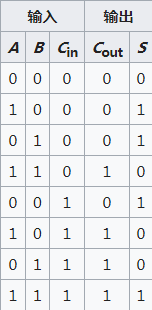 规则是
规则是
s = (x ^ y) ^ Cin
Cout = (x & y) | (y & Cin) | (x & Cin)
更简单的版本:
int getSum(int a, int b) {
return b == 0 ? a : getSum(a ^ b, (a & b) << 1);
}
不使用缓存交换整数
利用一个整数和自己进行异或运算会归0的性质
public int[] exchangeAB(int[] AB) {
AB[0] = AB[0] ^ AB[1];
AB[1] = AB[0] ^ AB[1]; // 只剩下AB[0]
AB[0] = AB[0] ^ AB[1]; // 只剩下AB[1]
return AB;
}
也可以使用加减法来操作
public int[] exchangeAB(int[] AB) {
AB[0] = AB[0] + AB[1];
AB[1] = AB[0] - AB[1]; // 只剩下AB[0]
AB[0] = AB[0] - AB[1]; // 只剩下AB[1]
return AB;
}