在很多语言中，字符char类型是八位, 那么可能取值有256种(-128 ~ -1, 0 ~ 127). 但是用二进制表示为0000 0000 ~ 1111 1111, 无符号整数的全部位都表示数值，而有符号数的最高位是符号位（0表示正数，1表示负数），所以实际表达数值的只剩下n-1位。这样理论上char的取值应该是1111 1111 = -127到0111 1111 = 127. 而-128 = 1 1000 0000需要9位来表达, 所以char是如何仅仅通过八位表达-128?
首先, 因为计算机只能做加法, 所以减法操作要转化为加法, 尝试将符号位参与运算, 1-1就转化为1 + (-1), 用二进制表达为0000 0001 + 1000 0001 = -2, 很明显是错的. 如果用原码表示, 让符号位也参与计算, 显然对于减法来说, 结果是不正确的. 这也就是为何计算机内部不使用原码表示一个数.
为了避免这种错误, 引入反码(正数的反码是其本身, 负数的反码是符号位不变, 其余位取反), 用-1的原码1000 0001的反码1111 1110来表达-1, 这样1 + (-1) = [0000 0001]反 + [1111 1110]反 = [1111 1111]反, 转为原码1000 0000 = -0. 发现用反码计算减法, 结果的真值部分是正确的.
二进制补码
为了彻底解决负数表达中的-0 = 0, 1000 0000 = 0000 0000问题, 引入补码(正数的补码是其本身，负数的补码为其反码加1). 补码是计算机中最常用的有符号数的表达形式。补码定义为最高位权重为负的二进制码。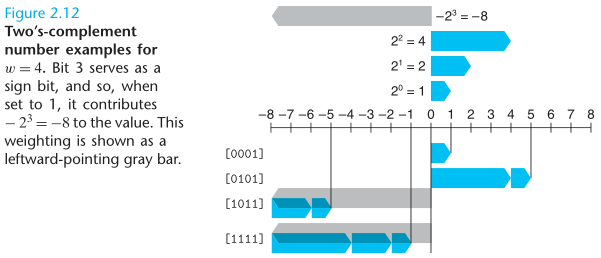
$$ B2T_4(0001) = -0 + 0 + 0 + 1 = 1 $$
$$ B2T_4(1111) = -8 + 4 + 2 + 1 = -1 $$
$$ B2T_4(0101) = -0 + 4 + 0 + 1 = 5 $$
$$ B2T_4(1011) = -8 + 0 + 2 + 1 = -5 $$
0 1 1 1 1 1 1 1 = 127 0 0 0 0 0 0 1 0 = 2 0 0 0 0 0 0 0 1 = 1 0 0 0 0 0 0 0 0 = 0 1 1 1 1 1 1 1 1 = −128 + 127 = -1 1 1 1 1 1 1 1 0 = −2 1 0 0 0 0 0 0 1 = −128 + 1 = -127 1 0 0 0 0 0 0 0 = −128
这样减法操作转化为加补码1+(-1) = [0000 0001]补 + [1111 1111]补 = [1 0000 0000]补, char定义为8位, 故第九位舍弃, 得到[0000 0000]补, 转换为原码为[1000 0000]原 = -0.
所以, -0 = [1000 0000]原的补码为1 0000 0000 = 0000 0000 = 0, 0 = 0000 0000的补码为1000 0000 = -0. 鉴于0的非负非正特性, 仅仅使用0000 0000来表达0和其补码就足够了. 这样1000 0000就可以挪作他用,用来表达-128. 之所以用来表达-128是有其合理性的. 因为-1 + (-127) = [1000 0001]原 + [1111 1111]原 = [1111 1111]补 + [1000 0001]补 = [1000 0000]补, -128 = 1 1000 0000的补码也刚好是1 1000 0000, 放进char的八位空间中, 需要把第九位截断, 得到的刚好是1000 0000.
可以推理出补码的取值范围，最小值为[10...0], $TMin_w = -2^{w-1}$, 最大值为[01...1], $TMax_w = 2^{w-1} - 1$. 使用补码, 不仅仅修复了0的符号以及存在两个编码的问题, 而且还能够多表示一个最低数. 这就是为什么8位二进制, 使用原码或反码表示的范围为[-127, +127], 而使用补码表示的范围为[-128, 127]. 同理16位short中-32768~32767，-32768原码为17位，丢弃最高位剩下的16和-0的原码相同。
可以观察到, abs(TMin) = TMax + 1 = TMin, 也就是最小值的绝对值还是最小值: -(INT_MIN) = - 0[1000 0000]补 = 1[1000 0000]补 = [1000 0000]补 = -128 = [0111 1111]补 + 1.
二进制补码运算是加法逆运算。补码系统的最大优点是可以在加法或减法处理中，不需因为数字的正负而使用不同的计算方式。只要一种加法电路就可以处理各种有号数加法，而且减法可以用一个数加上另一个数的补码来表示，因此只要有加法电路及补码电路即可完成各种有号数加法及减法。
Bitwise operators
Bitwise NOT - ~, or complement: 0 become 1, 1 become 0.
The bitwise complement is equal to the two’s complement of the value minus one.
~x = -x − 1
因为~x + x = b[1...1] = -1, 通过~x + 1得到一个数的负数, 得到的负数也就是该二进制数字的补码. 比如0 = b[0000], ~0 = b[1111],b[1111] + b[0001] = b[0000] = 0, 又比如TMin = b[1000], ~TMin = b[0111], ~TMin + 1 = b[0111] + b[0001] = b[1000] = TMin, 也就是-TMin = TMin.
Bitwise AND - &: 1 & 1 = 1, 1 & 0 = 0, 0 & 0 = 0.
performs the logical AND operation on each pair of the corresponding bits, which is equivalent to multiplying them. Thus, if both bits in the compared position are 1, the bit in the resulting binary representation is 1 (1 × 1 = 1); otherwise, the result is 0 (1 × 0 = 0 and 0 × 0 = 0).
Bitwise OR - |: 1 | 1 = 1, 1 | 0 = 1, 0 | 0 = 0
takes two bit patterns of equal length and performs the logical inclusive OR operation on each pair of corresponding bits. The result in each position is 0 if both bits are 0, while otherwise the result is 1.
Bitwise XOR - ^: 1 ^ 1 = 0, 1 ^ 0 = 1, 0 ^ 0 = 0
takes two bit patterns of equal length and performs the logical exclusive OR operation on each pair of corresponding bits. The result in each position is 1 if only the first bit is 1 or only the second bit is 1, but will be 0 if both are 0 or both are 1. In this we perform the comparison of two bits, being 1 if the two bits are different, and 0 if they are the same.
Bit shifts
Java中有三种移位运算符.
<<: 左移运算符，num << n, 把num的二进制左移n位, 右边的空位用0补上, 每一次移位相当于num * 2(除非overflow)>>: 右移运算符，num >> n, 右移n, 每次移位相当于num / 2- 如果是无符号数值，也就是
>>>，左边空缺用0补上, - 如果是有符号数值，则用数字的符号位填补最左边的
n位- 如果是正数, 则右移后在最左边补
n个0 - 如果原先是负数, 则右移后在最左边补
n个1
- 如果是正数, 则右移后在最左边补
- 如果是无符号数值，也就是