避免歧义的编码
在构建压缩编码的对应关系时,我们使用不同的数量的位来编码不同的字符.
比如摩斯密码 . 如果单纯使用这种对应关系,会出现一些问题, 如
. 如果单纯使用这种对应关系,会出现一些问题, 如•••−−−•••会产生歧义: SOS? V7? IAMIE? EEWNI? 所以在实际使用中, 密码使用一些间隔来分隔代码字。
那么对于不同的压缩编码, 有什么常用方法来避免歧义? 方法是确保没有一个编码是另一个编码的前缀。比如
- 使用固定长度编码。
- 为每个编码添加特殊的stop char。
- 使用一种具备广泛使用性的prefix-free编码。
用什么数据结构来设计prefix-free编码?
用Trie构造编码
一个二叉(0, 1)Trie: 叶节点是字符, 根节点到叶节点的路径就是编码.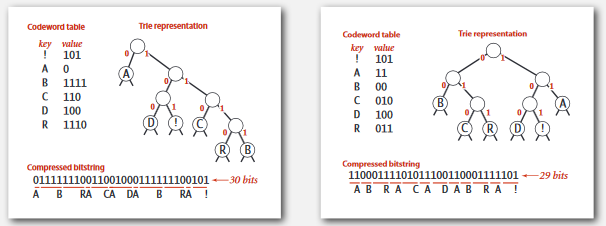
压缩:
方法1:从叶开始; 按照路径到达根; 反向打印bits。
方法2:创建键-值对的符号表。
解压:
- 从根节点开始, 根据位值是0还是1在Trie图上游走, 直到走到叶节点,则解压出一个字符
- 返回根节点, 继续第一步, 直到跑完所有编码.
private static class Node implements Comparable<Node>
{
private final char ch; // used only for leaf nodes
private final int freq; // used only for compress
private final Node left, right;
public Node(char ch, int freq, Node left, Node right)
{
this.ch = ch;
this.freq = freq;
this.left = left;
this.right = right;
}
public boolean isLeaf()
{ return left == null && right == null; }
// compare Nodes by frequency
public int compareTo(Node that)
{ return this.freq - that.freq; }
// Runtime - Linear in input size N
public void expand()
{
Node root = readTrie(); // read in encoding trie
int N = BinaryStdIn.readInt(); // read in number of chars
for (int i = 0; i < N; i++)
{
Node x = root;
while (!x.isLeaf())
{
if (!BinaryStdIn.readBoolean())
x = x.left;
else
x = x.right;
}
BinaryStdOut.write(x.ch, 8);
}
BinaryStdOut.close();
}
}
如何读取一个Trie:根据Trie的前序遍历序列重构.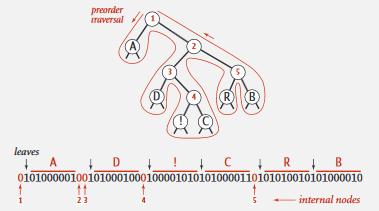
private static Node readTrie()
{
if (BinaryStdIn.readBoolean())
{
char c = BinaryStdIn.readChar(8);
return new Node(c, 0, null, null);
}
Node x = readTrie();
Node y = readTrie();
return new Node('\0', 0, x, y);
}
如何把Trie写为序列:以前序遍历的方式写Trie;额外用一个位标记是否叶节点。
private static void writeTrie(Node x)
{
if (x.isLeaf())
{
BinaryStdOut.write(true);
BinaryStdOut.write(x.ch, 8);
return;
}
BinaryStdOut.write(false);
writeTrie(x.left);
writeTrie(x.right);
}
用哈夫曼算法构建最优编码
就是用Huffman算法. Huffman算法是把最短的编码赋给出现频率最高的字符, 把最长的编码留给出现频率较低的字符. 在Trie上的效果就变成频率最高的字符路径最短, 长路径都留给频率低的字符. 这样总的效果就是使用了更少的数据位来表达同样的信息.
- 统计输入的各个字符的频率
freq[i]。 - 为每个
char i构建一个具有权重freq[i]的Trie(子节点为null), 从此节点开始 - 重复以下过程直到融合为一个trie(根节点):
- 选择当前权重最小的两Tries,
freq[i]和freq[j], 其中i <= j, freq[i] <= freq[j] - 给它们创建父节点, 权重为
freq[i] + freq[j], 两个子Trie和其父节点合并为一个Trie, 而且路径0(左边)总是指向较小的子Trie, 路径1(右边)指向较大的.
- 选择当前权重最小的两Tries,
private static Node buildTrie(int[] freq)
{
MinPQ<Node> pq = new MinPQ<Node>();
// initialize PQ with singleton tries
for (char i = 0; i < R; i++)
if (freq[i] > 0)
pq.insert(new Node(i, freq[i], null, null));
while (pq.size() > 1)
{ // merge two smallest tries
Node x = pq.delMin();
Node y = pq.delMin();
Node parent = new Node('\0', x.freq + y.freq, x, y);
pq.insert(parent);
}
return pq.delMin();
}
通过这个算法, 可以保证频率最高(权重最大)的字符的叶节点就是最左叶节点, 一般编码为0, 其他依次类推. 可以证明Huffman算法生成的最优prefix-free编码.
Implementation. ・Pass 1: tabulate char frequencies and build trie. ・Pass 2: encode file by traversing trie or lookup table
Running time. Using a binary heap ⇒ N + R log R. N input size, R alphabet size.
对于具有n个叶子节点的哈夫曼树,一共需要2*n-1个节点: 二叉树有三种类型节点,即子节点数为2的节点,为1的节点和为0的叶节点。而哈夫曼树的非叶子节点是由两个节点生成的,因此不能出现只有单子节点的节点,如果叶子节点个数为n, 那么非叶子节点的个数为n-1.
哈夫曼编码广泛应用于jpeg, pdf, MP3, MP4等文件编码中.
在神经网络中, 哈夫曼树也被用于构建层级Softmax.
一个使用Huffman Encoding的实例: https://github.com/congchan/cs106b-programming-abstraction/tree/master/HW6_Huffman%20Encoding/Huffman/src