虽然KMP可以用于单模式匹配问题,但如果是多模式问题, KMP的性能就得不到保证。比如根据墙内法律要求, 墙内的搜索引擎需要过滤敏感词后才能合法运营。敏感词的数量不少, 如果要求包含敏感词的网页不能被搜索到, 那么搜索引擎在爬取网页信息时, 就要标记网页的文本中是否包含任意个敏感词.
这就是典型的多模匹配问题. 这种情况下如果使用Trie,那么需要遍历网页的每一个字符位置,对每一个位置进行Trie前缀匹配。如果词典的词语数量为N,每个词语长度为L,文章的长度为M,那么需要进行的计算次数是在N*M*L这个级别的. 即使把词语的长度L简化为常数级别的, 整个算法的复杂度也至少是$O(n^2)$.
AC自动机
可以看到,KMP算法可以避免back up(在检查字符的过程中不需要回头),而Trie可以存储多个模式的信息。如果把二者结合在一起,也许能从性能上解决多模式(任意位置)匹配问题。这就是Aho–Corasick算法(AC自动机)。
Aho–Corasick算法是由Alfred V. Aho和Margaret J.Corasick 发明的字符串搜索算法,用于在输入的一串字符串中匹配有限组字典中的子串。它与普通字符串匹配的不同点在于同时与所有字典串进行匹配。算法均摊情况下具有近似于线性的时间复杂度,约为字符串的长度加所有匹配的数量。
所以算法的关键就是通过Trie把多个模式构建为一个DFA(Deterministic finite state automaton),然后让模式串末尾对应的状态作为一个DFA的终止节点。这样,对于一个要检查的长字符串(如一段网页内容),让这个字符串在DFA上跑一趟,每一个字符表示一种跳转方式,如果这段字符能够跳到任何一个终结节点, 那么就表明这段字符串匹配了至少一个模式, 如果整段字符跑完都没到达终结节点, 那么这个网页就是"和谐的".
在单模式匹配中, 用KMP构建的DFA是比较简单的, 从左到右, 开头的状态就是开始状态, 结尾的状态就是结束状态:
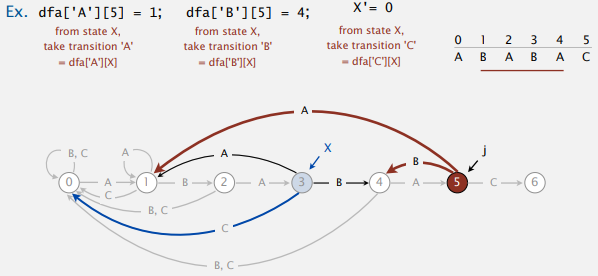 而多模式匹配中, 在Trie的结构基础上构建出来的DFA更像一个DFA的样子:
而多模式匹配中, 在Trie的结构基础上构建出来的DFA更像一个DFA的样子:
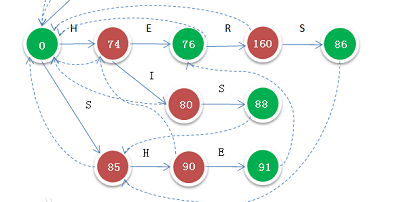 Trie中的节点, 就类似于DFA中的状态. 如果让字符串
Trie中的节点, 就类似于DFA中的状态. 如果让字符串shis在上面跑, 假如仅仅是靠Trie(也即是没有虚线标识的转移), 那么第一次从字符串的第一个字符s开始转移, 经过转移路径0 - 85 - 90之后就转不动了, 因为Trie记录的模式中没有shi, 这个时候得back up, 从第二个位置h开始再匹配一遍. 这个过程中就产生重复匹配, 而参考KMP的思路, 在匹配shi的过程中, 其实已经挖掘出了hi这个子串了, 而这个子串是跟模式his对应的, 如果有办法不回头继续匹配下去就能提高性能了.
而DFA中虚线的失败转移就是用来解决这个问题的: 当走到状态90时, 前面有了小部分子串h刚好对应状态74, 这个时候用虚线作为失败转移, 转移到74, 在状态74中寻找下一个转移i, 这样就实现了不回头继续匹配了.
因为AC自动机是在Trie的基础上添加边, 用于指示各个节点经过不同字符后跳转到哪个节点, 结果就变成了图, 所以也叫做Trie图.
要构建AC自动机:
- 首先要把所有模式都吃进一个Trie中(最近看多进击的巨人了), 构建出一个由不同实线串联起来的状态机, 其中代表刚好吻合一个模式的状态标记为终结节点(如上图绿色节点)
- 然后补全其他字符的转移(失败转移), 用虚线表示. 补全了所有字符的转移方式, 才能让字符串永不回头地匹配下去, 避免了back up, 保证性能.
问题的关键在如何补全所有的状态转移.
补全状态转移
 这里要在Trie结构中定义一个后缀节点的概念: Trie中对应路径(已有模式)去掉部分前缀字符后剩余的后缀字符在Trie中对应的结点. 比如上图中,
这里要在Trie结构中定义一个后缀节点的概念: Trie中对应路径(已有模式)去掉部分前缀字符后剩余的后缀字符在Trie中对应的结点. 比如上图中, h作为sh的一个后缀, h对应的Trie节点74就是sh对应节点90的后缀节点. 等于说, 节点和其后缀节点对应的模式有一部分后缀是相同.
如果知道了每一个节点的后缀节点, 那么在匹配的过程中, 在任一位置匹配失败, 都可以通过失败转移的方式转移到后缀节点, 继续进行后续匹配, 而不会遗漏, 因为后缀节点对应这个目前为止已匹配字符的某一部分后缀. 等于说, 后缀节点告诉我们, 在字符串中出现与模式不同的字符串时(匹配失败), 如何转移到其他状态.
所以问题的关键又变成了如何求后缀节点.
求后缀节点
观察Trie结构可以发现两个要点
- 字符串任何一个位置对应的状态节点,一定比它的后缀节点更深,比如前面例子中状态节点
90在第二层, 而其后缀节点74在第一层. 这点也是理所当然的, 毕竟后缀比较短. 从动态规划的角度考虑, 字符串任一位置i对应的状态节点的后缀节点一定是k<i的节点中的某一个. - 因为每一个状态
i都是由其父节点j通过某一个字符c转移而来, 那么i的后缀节点一定是j的后缀节点通过同样的字符c转移而来. 或者说, 如果j的后缀节点是jj, 那么j和jj有着相同的后缀, 它们通过同样的转移字符c转移后, 二者到达的节点也一定有着相同的后缀.
比如上面Ushers自动机例子中, 如果用字符串sshis来跑, 那么ssh对应的状态90, 是由前缀ss通过字符h转移而来. 因为ssh的后缀节点, 同样是某一个有共同后缀的字符(h或者sh)对应的状态(在这里是h对应的74). 可以发现74是由根节点0通过同样的字符h转移而来的. 反过来说, 节点0就是节点90的父节点85的后缀节点.
在多个模式中, 如果有某模式的前缀刚好是另一模式的子串(后缀). 比如上面Ushers自动机例子中, 模式her(或者he)的前缀he就是模式she的子串, 则会二者存在失败转移的关联. 如果没有, 那么就跳回初始状态节点.
所以补全所有状态转移的具体实现方法就是运用动态规划的原理:
- 从Trie根节点开始, 逐层往下补全每一层的状态转移, 也就是宽度优先遍历(BFS), 这样下层的状态转移就可以利用上层的结果. 动态规划的转移方程可以描述为: 每一个通过字符
c转移而来的状态节点i的后缀节点 =i的父节点的后缀节点通过c转移到的状态节点 - 初始状态包含两部分:
- 一个是根节点(初始状态
0), 它的后缀节点就是它自己, - 另一个是第一层的状态节点, 如
85, 74, 因为它们对应的是长度为1的字符, 没有后缀, 所以它们的后缀节点也是根节点0.
- 一个是根节点(初始状态
在实现中还要注意, 后缀结点为标记结点的结点也需要被标记. 因为在状态转移过程中, 如果某个虚线转移刚好转移到终结节点, 但在字符串遍历的过程中, 并没有选择走这一条线, 就会忽略了这个终结节点, 导致匹配失败, 或者多走了更多的路. 比如在上面的例子中, 如果把模式she改为shee, 91不再是终结节点, 而是延伸到92为终结节点, 91的后缀节点是76. 如果用字符串sshe来跑这个DFA, 就会出现走到最后字符e时, 在节点91结束, 匹配失败. 所以需要把91也标记为终结节点.
实现代码
/** 把字典通过insert把所有单词插入Trie树,
* 然后通过setSuffix()构建出对应的Trie图,
* 然后从Trie图的根节点开始,沿着文章str的每一个字符,走出对应的边,
* 直到遇到一个标记结点或者整个str都遍历完成
*/
public static class Trie {
private TrieNode trie;
Queue<TrieNode> queue;
public Trie() {
trie = new TrieNode(null, ' ');
queue = new LinkedList<>();
}
public void insert(String word) {
TrieNode curNode = trie;
for (char x : word.toCharArray()) {
curNode = insert(curNode, x);
}
curNode.setLast(true);
}
/** insert char x, means create a new node in the x edge.
* return created node */
private TrieNode insert(TrieNode node, char x) {
if (node.get(x) == null) {
node.set(x);
}
return node.get(x);
}
/** BFS on the trie */
public void setSuffix() {
queue.add(trie);
while (!queue.isEmpty()) {
/** poll() removes the present head.
http://www.tutorialspoint.com/java/util/linkedlist_poll.htm */
TrieNode node = queue.poll();
setSuffix(node);
complementDFA(node);
}
}
/** Set node's suffix, complement lacking edge
* */
private TrieNode setSuffix(TrieNode node) {
if (node.root == null) { // Trie root
node.suffix = node;
} else if (node.root.root == null) {
node.suffix = node.root.suffix;
} else {
node.suffix = node.root.suffix.get(node.fromIndex);
}
if (node.suffix.isLast) {
node.isLast = true;
}
return node.suffix;
}
/** Complement DFA according to suffix */
private void complementDFA(TrieNode node) {
if (node.isLast) { return; }
for (int i = 0; i < node.edges.length; i++) {
if (node.edges[i] == null) {
if (node.root == null) {
node.edges[i] = node;
} else {
node.edges[i] = node.suffix.edges[i];
}
} else {
queue.add(node.edges[i]);
}
}
}
public boolean search(String s) {
boolean contains = false;
TrieNode curNode = trie;
for (int i = 0; i < s.length(); i++) {
char x = s.charAt(i);
curNode = curNode.get(x);
if (curNode.isLast) {
contains = true;
break;
}
}
return contains;
}
public static class TrieNode {
static final int R = 26;
static final int ATO0 = 97;
boolean isLast;
TrieNode[] edges;
TrieNode root;
char fromIndex;
TrieNode suffix;
public TrieNode(TrieNode root, char from) {
this.root = root;
fromIndex = from;
edges = new TrieNode[R];
isLast = false;
}
public TrieNode get(char ch) {
return edges[ch - ATO0];
}
/** instantiate the ch child in edges */
public void set(char ch) {
edges[ch - ATO0] = new TrieNode(this, ch);
}
public void setLast(boolean isLast) {
this.isLast = isLast;
}
}
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
Trie t = new Trie();
String[] X = {"sb", "dsb", "cjdsb", "qnmlgb"};
for (String x : X) {
t.insert(x);
}
t.setSuffix();
String s = "aadbaaadaaac";
if (t.search(s)) {
System.out.println("YES");
} else {
System.out.println("NO");
}
}
}