针对样本不平衡问题,除了上下采样,调整样本权重等统计方法,还有可以通过对loss函数进行设计。
对于多分类问题(n选1),一般使用softmax;对于多标签分类问题(n选k),一般是转换为n各sigmoid二分类问题。
Hierarchical classification
Yolo2里提出了Hierarchical classification方法,大概思路就是利用标签的结构关系建立wordtree,对标签划分层次,再在每个层次中做Data Augmentation,达到局部平衡,再进行局部softmax。
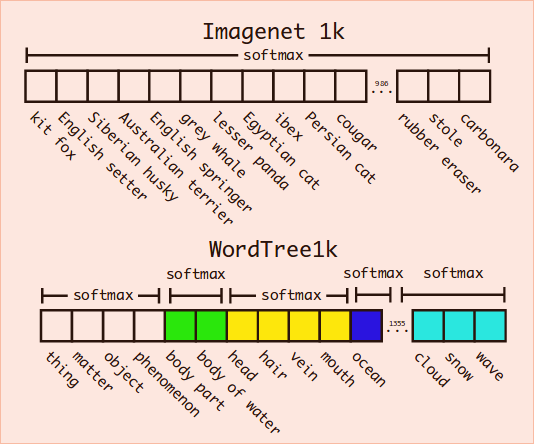
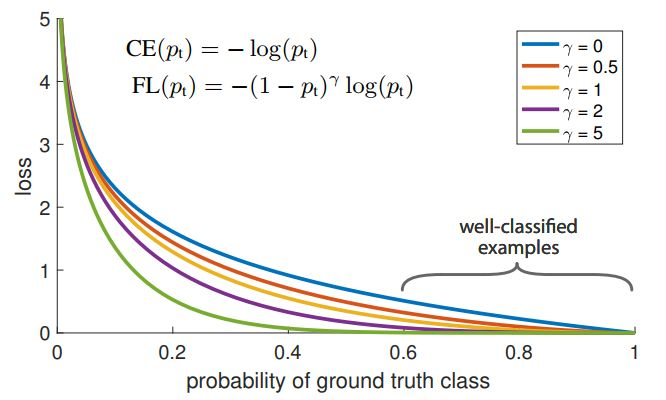
Focal Loss
Focal Loss for Dense Object Detection
- 极度不平衡的正负样本比例: anchor近似于sliding window的方式会使正负样本接近1000:1,而且绝大部分负样本都是easy example,
- 这就导致**gradient被easy example dominant的问题:**往往这些easy example虽然loss很低,但由于数量众多,对于loss依旧有很大贡献,从而导致收敛到不够好的一个结果。
- 按照loss decay掉那些easy example的权重,这样使训练更加bias到更有意义的样本中去。
实现: https://github.com/congchan/nlp/blob/e5cb1405b21245ad6cfe1f71a9961b6519e4e618/torch/loss.py#L5
def sigmoid_focal_loss(
inputs: torch.Tensor,
targets: torch.Tensor,
mask: torch.Tensor = None,
alpha: float = 0.25,
gamma: float = 2,
reduction: str = "none",
):
"""
Original implementation from https://github.com/facebookresearch/fvcore/blob/master/fvcore/nn/focal_loss.py .
Loss used in RetinaNet for dense detection: https://arxiv.org/abs/1708.02002.
Args:
inputs: A float tensor of arbitrary shape.
The predictions for each example.
targets: A float tensor with the same shape as inputs. Stores the binary
classification label for each element in inputs
(0 for the negative class and 1 for the positive class).
mask:
alpha: (optional) Weighting factor in range (0,1) to balance
positive vs negative examples or -1 for ignore. Default = 0.25
gamma: Exponent of the modulating factor (1 - p_t) to
balance easy vs hard examples.
reduction: 'none' | 'mean' | 'sum'
'none': No reduction will be applied to the output.
'mean': The output will be averaged.
'sum': The output will be summed.
Returns:
Loss tensor with the reduction option applied.
"""
p = torch.sigmoid(inputs)
ce_loss = F.binary_cross_entropy_with_logits(
inputs, targets, reduction="none"
)
p_t = p * targets + (1 - p) * (1 - targets)
loss = ce_loss * ((1 - p_t) ** gamma)
if alpha >= 0:
alpha_t = alpha * targets + (1 - alpha) * (1 - targets)
loss = alpha_t * loss
if mask is not None:
loss = torch.einsum("bfn,bf->bfn", loss, mask)
return loss
Circle Loss
A Unified Perspective of Pair Similarity Optimization
着眼点就是在multiple positive情况下该如何改造softmax的问题
公式1提供的unfied视角是很重要的。它允许我们不经过任何modification,用完全相同的一个数学表达,兼容pairwise learning和classification learning两种基本的深度特征学习方式。
单标签分类的交叉熵
$-\log \frac{e^{s t}}{\sum_{i=1}^{n} e^{s_{i}}}=-\log \frac{1}{\sum_{i=1}^{n} e^{s_{i}-s_{t}}}=\log \sum_{i=1}^{n} e^{s i-s t}=\log \left(1+\sum_{i=1, i \neq t}^{n} e^{s i-s t}\right)$
其中的 LogSumExp 是max的smoothing, 实现了“目标类得分都大于每个非目标类的得分”的效果
有多个目标类的多标签分类场景: 也希望“每个目标类得分都不小于每个非目标类的得分”, 于是
$\log \left(1+\sum_{i \in \Omega_{n e g}, j \in \Omega_{p o s}} e^{s_{i}-s_{j}}\right)=\log \left(1+\sum_{i \in \Omega_{n e g}} e^{s_{i}} \sum_{j \in \Omega_{p o s}} e^{-s_{j}}\right)$
其中的 $\Omega_{pos}, \Omega_{n e g}$分别是正负样本的类别集合, 这个loss的目标就是让 $s_{i}

对于分类问题, 不考虑$\gamma$和m, 对于k不固定的多标签分类来说,我们就需要一个阈值来确定输出哪些类。为此,我们同样引入一个额外的0类,希望目标类的分数都大于$s_0$,非目标类的分数都小于$s_0$,希望$s_i < s_j$就往$log$里边加入$e^{s_i − s_j}$,所以现在上面的多个目标类的多标签分类场景公式变成:
$\begin{aligned} & \log \left(1+\sum_{i \in \Omega_{n e g}, j \in \Omega_{p o s}} e^{s i-s j}+\sum_{i \in \Omega_{n e g}} e^{s i-s 0}+\sum_{j \in \Omega_{p o s}} e^{s_{0}-s j}\right) \\\\ =& \log \left(e^{s_{0}}+\sum_{i \in \Omega_{n e g}} e^{s_{i}}\right)+\log \left(e^{-s_{0}}+\sum_{j \in \Omega_{p o s}} e^{-s_{j}}\right) \end{aligned}$
如果指定阈值为0,那么就简化为
$\log \left(1+\sum_{i \in \Omega_{n e g}} e^{s i}\right)+\log \left(1+\sum_{j \in \Omega_{p o s}} e^{-s j}\right)$
最终得到的Loss形式了——“softmax + 交叉熵”在多标签分类任务中的自然、简明的推广,它没有类别不均衡现象,因为它不是将多标签分类变成多个二分类问题,而是变成目标类别得分与非目标类别得分的两两比较,并且借助于LogSumExp的良好性质,自动平衡了每一项的权重。
def multilabel_categorical_crossentropy(y_true, y_pred):
"""多标签分类的交叉熵
说明:y_true和y_pred的shape一致,y_true的元素非0即1,
1表示对应的类为目标类,0表示对应的类为非目标类。
警告:请保证y_pred的值域是全体实数,换言之一般情况下y_pred
不用加激活函数,尤其是不能加sigmoid或者softmax!预测
阶段则输出y_pred大于0的类。如有疑问,请仔细阅读并理解
本文。
"""
y_pred = (1 - 2 * y_true) * y_pred
y_pred_neg = y_pred - y_true * 1e12
y_pred_pos = y_pred - (1 - y_true) * 1e12
zeros = K.zeros_like(y_pred[..., :1])
y_pred_neg = K.concatenate([y_pred_neg, zeros], axis=-1)
y_pred_pos = K.concatenate([y_pred_pos, zeros], axis=-1)
neg_loss = K.logsumexp(y_pred_neg, axis=-1)
pos_loss = K.logsumexp(y_pred_pos, axis=-1)
return neg_loss + pos_loss
Max函数smoothing:LogSumExp
Softmax中使用的LogSumExp函数是max函数的一个平滑近似:
$LSE(\mathbf{x} ; \gamma)=\frac{1}{\gamma} \log \sum_{i} \exp \left(\gamma x_{i}\right) \approx \max (\mathbf{x})$
其中 $\gamma$ 越大,近似效果越好。通过加一个负号,我们可以使LSE也能够近似min函数:
$N L S E(\mathbf{x} ; \gamma)=-\frac{1}{\gamma} \log \sum_{i} \exp \left(-\gamma x_{i}\right) \approx \min (\mathbf{x})$
类似的有,softplus函数是relu函数的一个近似:
$\text { Softplus }(x)=\log (1+e^x) \approx \max (x, 0)=[x]_+$
利用这两个公式来改写一下公式(1):
(Hugo无法解析该公式)从知乎1上截图如下:
对比AM Softmax做同样转化后的形式
$$L_{a m} \approx \gamma\left[\max \left(s_{n}\right)-s_{p}+m\right]_{+}$$$L_{uni}$ 用 $min(s_p)$ 代替了 $L_{am}$ 里单个的 $s_p$
AM Softmax的目标函数用文字描述是:
使同类相似度比最大的非同类相似度更大。
类似的,替代之后的文字描述变为:
使最小的同类相似度比最大的非同类相似度更大。
这个说法也等价于:
所有同类相似度都比所有非同类相似度更大。
不管哪个说法: 让同类相似度与非同类相似度之间拉开一定的margin。
LogSumExp 函数有一个很有意思的性质:它的梯度恰好是softmax函数。也就是说,LSE的梯度是按softmax的指数下降来分配的。而从上边的公式可以看出,不论拿到多少梯度,也都会拿到同等大小的相反的梯度。实际上这个损失函数不管K和L的差距有多大,同类和非同类的相似度都会拿到一样多的梯度,保持了梯度平衡性。
Softmax实际上并不是max函数的smooth版,而是one-hot向量(最大值为1,其他为0)的smooth版。
使用神经网络进行多分类(假设为 [公式] 类)时的目标函数是什么?
输出C个分数,使目标分数比非目标分数更大。
设 $z=f(x) \in \mathcal{R}^{C}$,y为真值标签的序号,优化目标为 $\forall j \neq y, z_{y}>z_{j}$
如何优化?我们可以给 Zy 一个负的梯度,给其他所有 Zj 一个正的梯度,经过梯度下降法,即可使 Zy 升高而 Zj 下降。为了控制整个神经网络的幅度,不可以让 Z 无限地上升或下降,所以我们利用max函数,让 Zy 刚刚超过 Zj 时就停止上升:
$$\mathcal{L}=\sum_{i=1, i \neq y}^C \max \left(z_i-z_y, 0\right)$$然而在训练集上才刚刚让 Zy 超过 Zj,那测试集很可能就不会超过, 这样做往往会使模型的泛化性能比较差。借鉴svm里间隔的概念,我们添加一个参数,让 Zy 比 Zj 大过一定的数值才停止:
$$\cal L_{hinge} =\sum_\{i=1, i \neq y}^C \max \left(z_{i} - z_{y} + m, 0\right)$$如果直接把hinge loss应用在多分类上的话,当类别数C特别大时,会有大量的非目标分数得到优化,这样每次优化时的梯度幅度不等且非常巨大,极易梯度爆炸。
其实要解决这个梯度爆炸的问题也不难,我们把优化目标换一种说法:
输出C个分数,使目标分数比最大的非目标分数更大。
跟之前相比,多了一个限制词“最大的”,但其实我们的目标并没有改变,“目标分数比最大的非目标分数更大”实际上等价于“目标分数比所有非目标分数更大”。这样我们的损失函数就变成了:
$$\cal L=\max \left( \max_\{i \neq y} \\{z_i \\}-z_y, 0\right)$$在优化这个损失函数时,每次最多只会有一个+1的梯度和一个-1的梯度进入网络,梯度幅度得到了限制。但这样修改每次优化的分数过少,会使得网络收敛极其缓慢. 需要平滑,使用LogSumExp函数取代max函数:
$$\cal L_{l s e}=\max \left(\log \left(\sum_\{i=1, i \neq y}^C e^{z_i}\right)-z_y, 0\right)$$LogSumExp函数的导数恰好为softmax函数
$$\frac{\partial \log \left(\sum_{i=1, i \neq y}^{C} e^{z_{i}}\right)}{\partial z_{j}}=\frac{e^{z_{j}}}{\sum_{i=1, i \neq y}^{c} e^{z_{i}}}$$经过这一变换,给予非目标分数的1的梯度将会通过LogSumExp函数传播给所有的非目标分数,各个非目标分数得到的梯度是通过softmax函数进行分配的,较大的非目标分数会得到更大的梯度使其更快地下降。这些非目标分数的梯度总和为1,目标分数得到的梯度为-1,总和为0,绝对值和为2,这样我们就有效地限制住了梯度的总幅度。
LogSumExp函数值是大于等于max函数值的,而且等于取到的条件也是非常苛刻的(具体情况还是得看我的博士论文,这里公式已经很多了,再写就没法看了),所以使用LogSumExp函数相当于变相地加了一定的 m。但这往往还是不够的,我们可以选择跟hinge loss一样添加一个 m,那样效果应该也会不错,不过softmax交叉熵损失走的是另一条路:继续smooth。