字符搜索匹配算法 01 - Knuth–Morris–Pratt(KMP)

In computer science, string-searching algorithms, sometimes called string-matching algorithms, are an important class of string algorithms that try to find a place where one or several strings (also called patterns) are found within a larger string or text.

字符串搜索/匹配算法在大规模文本应用中有非常重要的作用，比如文章敏感词搜索，多关键词过滤搜索等。如果使用暴力搜索，则时间复杂度很高（若 m 为关键字的长度， n 为要待搜索的字符串长度， k为关键字数量，则复杂度为$O(n \times m \times k)$。而好的算法可以让这些问题的时间复杂度大大降低。

常用的算法有Knuth–Morris–Pratt(KMP), Boyer-Moore(BM), Rabin-Karp(RK), Trie, Trie图, AC自动机等.

一个实例

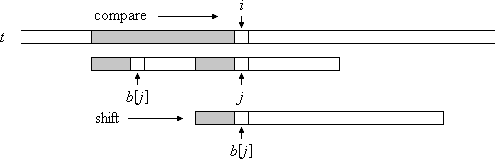
匹配时，想象我们拿着模式字符串pat=ABABAC, 像尺子一样从左到右对齐依次匹配如图的txt。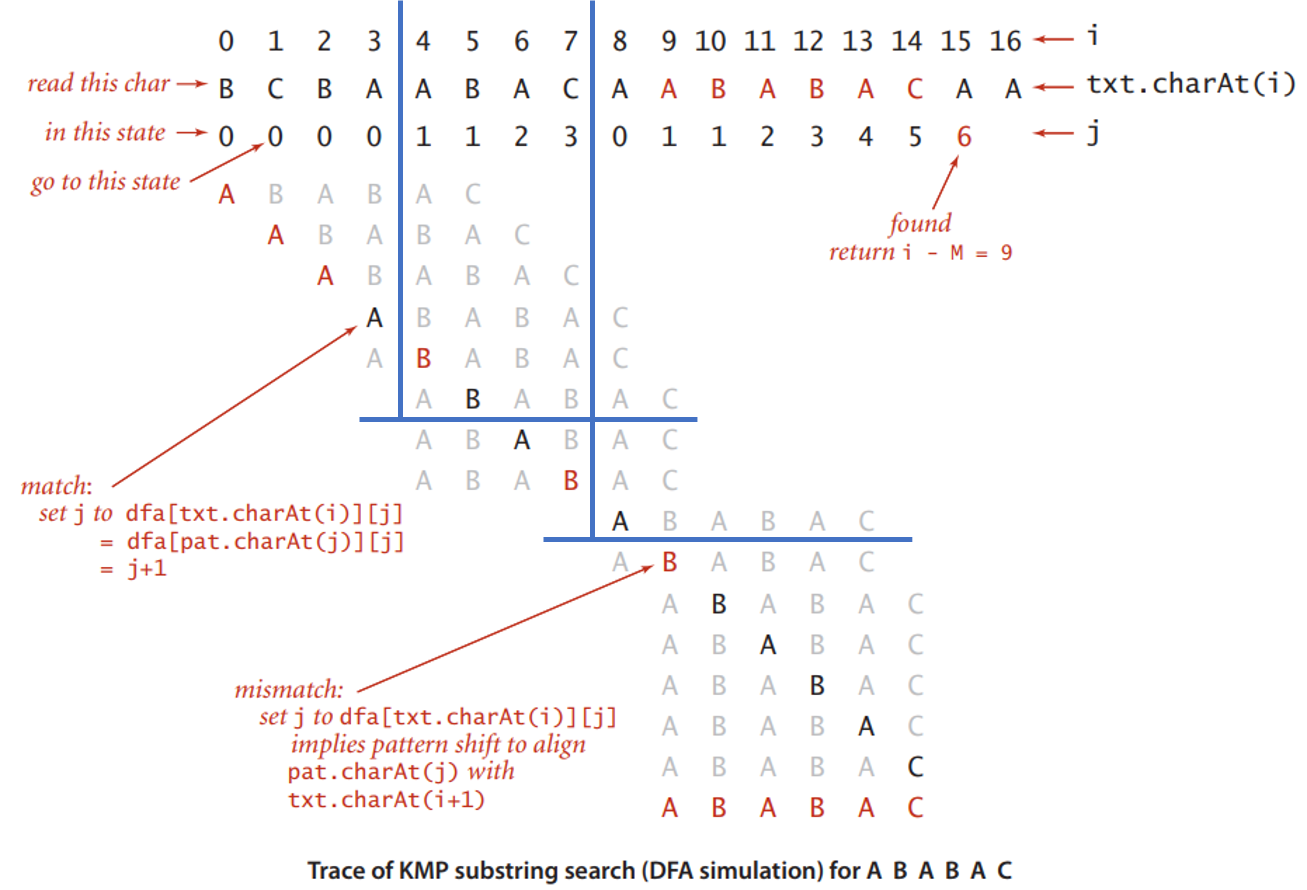

从txt[i=0]开始, 把pat的开头pat[j=0]对齐txt[0], 开始比较pat[0]和txt[0],

发现不匹配, 暴力的算法是从txt下一个字符重新开始i=1, 同时把尺子也右移一位对齐新的txt起始点.
从i=3开始, 发现一开始可以匹配上(pat[j=0] == txt[3]), 那么保持尺子不动, 开始比较pat[j+1]和txt[i+1], 结果不匹配.
从i=4开始, 情况也类似, 而且发现连续匹配上了pat[++j]和txt[++i], 假如运气好, 我们能匹配完整个尺子, 那么达到目的. 可惜在i=7时失败了.
问题的关键就是i=3和i=7这里, 特别是i=7, 假如还是用暴力解法1操作, 那么需要重新比对txt[i=5,6,7...]. 但前面已经匹配了一半的尺子了, 那么其实我们已经知道了txt的后缀txt[4,5,6]和尺子的前缀pat[0,1,2]重合, 我们能否利用这个信息来优化算法?

按照前面的分析, 每一个已匹配的前缀等于txt中已匹配的后缀, 那么txt后缀后面可能接的字符有R种, 我们可以提前计算每一个已匹配txt后缀后接每一种字符时, 应该怎么做.

自动机匹配字符

我们可以建立一个有限自动机，该自动机会扫描文本字符串T以查找模式P的所有出现。这些字符串匹配自动机非常高效：只对每个文本字符检查一次，每个文本字符花费固定的时间, 匹配开销是O(n)。但是需要预处理pattern以构建自动机。

为了方便说明, 先定义一个有关对应 pattern $P$的后缀函数(Suffix function)$\sigma(x)$, 该函数返回$P$和字符串$x$的后缀重叠的最长前缀的长度.

比如对于$P = ab$, $\sigma(ccaca) = 1$, $\sigma(ccab) = 2$, 空字符$\epsilon$可以是任何字符的前缀, $\sigma(\epsilon) = 0$,

定义自动机用于读取字符串:

自动机的状态$\Phi(w)$表示读取字符$w$后达到的状态$M$, $\Phi (\epsilon) = q_0$.
定义自动机的有限状态集为${0, 1, …, m}$, 起始状态$q_0 = 0$, 最终接收状态是$m$;
设置转移函数$\delta$为$\delta(q, a) = \sigma(P_qa)$, 这么定义是为了追踪当前已经匹配的pattern最长前缀. $\Phi (wa) = \delta(\Phi(w), a)$

该自动机满足不变性 $\Phi(T_i) = \sigma(T_i) = q$. 那么当自动机在状态q时读入下一个条件字符T[i+1] = a, 自动机要把状态转移到和$T_ia$的后缀匹配的$P$最长前缀对应的状态$\sigma(T_ia)$. 因为$P_q$是$P$和$T_i$的后缀匹配的最长前缀, 因此不严谨地推理出$\sigma(T_ia) = \sigma(P_qa)$.

DFA KMP

Knuth版本的KMP算法, 就是用**确定性有限自动机（Deterministic Finite Automaton, DFA）**来匹配字符：

有限数量的状态（包括开始和停止）, 中间状态对应txt的后缀和pattern的重叠。
确定性: 字母表每个字符对应一个状态转移, 每个状态转移都对应一个确定的字符。
只接受能通往停止状态的转换序列。

DFA以dfa[i][j]状态矩阵的数据结构应用于KMP算法,

每一行对应一种字符, 字符指示了跳转的条件
每一列对应一种后缀: 第j列的含义是, txt后缀已经匹配了pat[..., j-1]后根据各行条件字符所应跳转到的状态
每一列只有一个字符行是匹配跳转, 匹配跳转永远是跳转到j+1状态(列), 其他都是不匹配跳转.
确定性状态: j = 0..len(pat), 在DFA的各个确定性状态中跳转, 保证了当前不管处于哪个状态, j等于已经成功匹配的pattern前缀长度, 也就是pattern的前缀pattern[0...j]刚好是txt的最长匹配后缀txt[0..i].

匹配的过程, 被抽象为把txt的字符从左到右依次输入DFA, 并根据每次读入的字符决定跳去哪个状态, 如果能够到达终点状态, 那就是有一个完整的匹配.

如ABCAABABABAB对应0→1→2→0→1→1→2→3→4→5→4→5→4

在匹配的过程中, 假设已经对比了txt[i]和pat[j], 那么state = dfa[txt[i]][j]就是转移到下一个状态state, 接下来需要对比txt[i+1]和pat[state].

如果匹配, 那么只需要继续检查txt下一个字符i++, 此时我们要求dfa[pat.charAt(j)][j] = j+1, 也就是和pattern的下一个字符对比.
如果不匹配, 我们不仅已经知道了txt[i], 也知道了txt的后j-1个字符刚好是pattern的前j-1个字符

回到这个实例中: 在遇到不匹配时, 有了dfa就可以知道在ABA_后面分别遇到A, B和C时应该如何对齐尺子, 同时不需要回溯, 也就是i++. 比如i=7时, 是属于ABA_接C, 对应dfa[C][3]=0, 同时把尺子的开头对齐到i=8, 继续比对就好了, 不用担心前面txt[5,6,7]会不会遗漏什么.

public int search(String txt)
{
	int i, j, N = txt.length();
	for (i = 0, j = 0; i < N && j < M; i++)
		j = dfa[txt.charAt(i)][j];
	if (j == M) return i - M; // found
	else return N; // not found
}

Running time: at most N character accesses to Simulate DFA on text.

KMP因为保证了字符串遍历指针只会前进不会后退, 所以可以接受stream输入.

构建DFA

首先需要了解DFA状态矩阵的特性, 那就是每一列的状态j只能在0到j+1转移, 也就是只能在第一列和右边相邻一列之间跳转. 这个特性, 和匹配过程中pattern的移位对齐方式一致. 抽象的DFA只能从左往右逐个生成状态. 所以我们从左往右生成/完善DFA, 也就说从左列往右列构建dfa[][]矩阵. 在构建第j个状态时, 我们只需要知道DFA如何读取前j-1个字符进行转移，因此我们始终可以从前面部分构建的半成品DFA中获得下一步状态所需的信息。

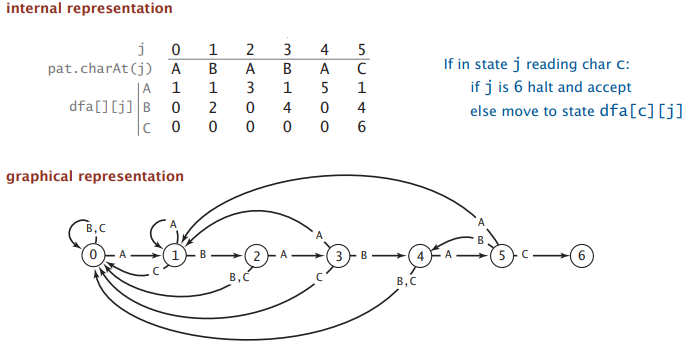
对于patternABABAC, 其5个前缀列表的跳转方向对应了DFA的5个状态0, ..., 5.

第一列(状态0)也就是对应的前缀pat[-1] = ...在遇到pat[0] = A时才能前进, 其他行都是维持原状态0不变.
关键是如何确定其他不匹配字符的跳转状态

j   0 1 2 3 4 5
    A B A B A C
  -------------
A | 1 - 3 - 5 -
B | 0 2 - 4 - -
C | 0 - - - - 6

设想DFA还在构建中, 只是刚刚完成第一列. 此时可应对匹配pattern至多前两个前缀(...和A...)的情况.

然后我们需要构建第1列:

设想如果txt[...i]的后缀匹配了前缀pat[j-1] = A...后, 进入了状态dfa[A][0] = 1, 但此时1列还没构建; 如果下一个字符txt[i+1]=C和pat[j]对比发现不匹配时，我们需要在DFA此时状态栏dfa[C][1]存储正确的跳转. 如何得出正确跳转? 就是其转移目标等同于用暴力算法得到结果. 暴力算法选择用txt[i+1]和pat[0]比对, 此时等价于把txt[i+1] = C输入当前构建中的DFA, 会定位到dfa[C][0], 跳转到0. 这个过等价于给txt后缀txt[i+1] = ...AC寻找和pattern重叠的前缀...(没有重叠, 状态0), 等于pattern开头移位对齐到txt[i+2].

此时的DFA虽然还是半成品, 只包含了pat[0]这部分信息, 却可以据此推测出pat[.][1]的信息;

同理, 假如txt[i+1]=A, 可以推测出pat[A][1] = dfa[A][0] = 1; 这样我们就推理出了DFA第二个状态在R字符空间的所有确定性转移.

    X
    ↓
j   0 1 2 3 4 5
    A B A B A C
  -------------
A | 1 1 3 - 5 -
B | 0 2 - 4 - -
C | 0 0 - - - 6

如果用X临时变量来存储上一次复制的状态(0), 那么上面的操作概括为dfa[c][j] = dfa[c][X];, 其中j代表当前待构建的状态列, c代表不匹配的条件字符. 这里X也指示了pattern移位对齐的位置, 在Robert Sedgewick的书中, 也把这种对齐称之为DFA restart position.

依次类推…

假设我们推理到状态5, (根据前面的流程此时X=3), 同样设想txt[i, ..., i+4]后缀已经匹配了前缀pat[0, ..., j-1] = ABABA...后, 假如下一个字符txt[i+5]=B和pat[j]对比不匹配. 暴力检索需要回溯后缀txt[i+1, ..., i+4] = ...BABA, 输入DFA可定位到状态3, 然后复制dfa[B][3] = 4; pattern和txt后缀txt[i+1, ...] = ...BABAB重叠的前缀是ABAB..., 直接可推测出移位pattern和txt[i+6]对齐的索引是4.

总结算法: 构建每一个状态state j时, 表示模式pat的前j个字符已经匹配. 用dfa[r][j]表示在状态state j时, 遇到下一个字符r时应该转移到哪个状态：

对于不匹配的字符，copy dfa[][X] to dfa[][j].
对于匹配的字符，dfa[pat.charAt(j)][j] = j+1.
Update X.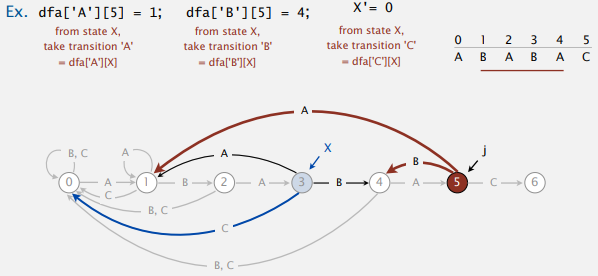

public dfaKMP(String pat)
{
	this.pat = pat;
	M = pat.length();
	dfa = new int[R][M];
	dfa[pat.charAt(0)][0] = 1;
	for (int X = 0, j = 1; j < M; j++)
	{
		for (int c = 0; c < R; c++)
			dfa[c][j] = dfa[c][X]; // copy mismatch cases
		dfa[pat.charAt(j)][j] = j+1; // set match cases
		X = dfa[pat.charAt(j)][X]; // update restart state
	}
}

Running time. M character accesses (but space/time proportional to R M).

NFA KMP

Knuth版本的KMP问题是当R也就是字符集较大时, 比如有一个像Unicode这样的字符集，即使pattern仅由几个不同的字母组成，存储该DFA所需的内存也会很大。

改进方法是由Knuth的学生Pratt提出的用**非确定性有限自动机（Non-deterministic Finite Automaton, NFA）**来解决. 既然导致DFA矩阵过大的原因是字符集R过大, 那么可否考虑把所有not match的字符归为一种不匹配转移? 这样在FSM中，任何状态下都只有两种转移：匹配和不匹配。很容易看出，所需的额外空间相对于M（pattern的长度）是线性的。这个版本的KMP算法就是最后三位作者联名发表的论文呈现的方法.

代价就是当出现不匹配字符时无法保证确定性, 因为导致不匹配的字符有很多种, 所以是一种NFA。因为状态序列和pattern序列一一对应, 而且只有两种状态转移, 其中一种是确定性的, 确定性的转移永远是text[i] == pat[j], state += 1, 所以只需要保存不匹配状态转移, 也就是用一维数组保存在每一个状态遇到不匹配时应该转移到哪一个状态.

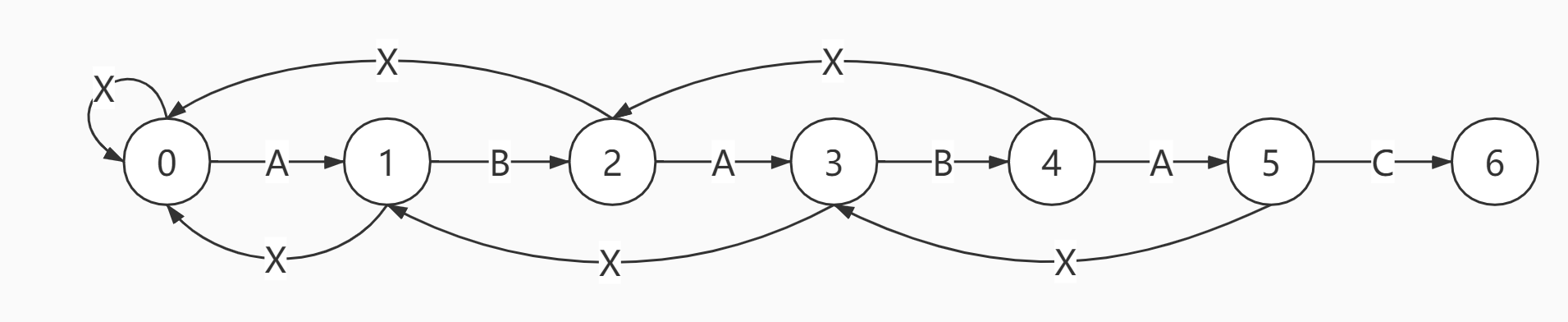
Border

不匹配时如何转移是nfa模型的关键. KMP使用一个辅助数组提前存储有关pattern自身的信息(这种信息称之为Border), 以达到在线计算自动机转移函数的目的. 定义一个有关pattern $P$的Border(或者称之为Prefix function), 该函数封装了有关$P$如何匹配偏移的$P$的知识。

比如这种情况:

0 1 2 3 4 5 6 7 8 9 ...
a b c a b c a b d  
a b c a b d     
      a b c a b d

如果提前知道了pattern[...,4]的后缀ab和其前缀一样, 那么就可以直接把重合的前缀移位对齐过去. 也就是需要提前计算pattern每一个前缀p[...i]的前后缀重复情况.

构建patternABABAC的前缀列表, 根据索引位置分别编号为0...6: 0 ε... 什么都没匹配 1 A... 2 AB... 3 ABA... 4 ABAB... 5 ABABA... 6 ABABAC 完全匹配

每一个前缀自身都可能存在前后缀重复的情况. 比如前缀ABAB...就有前后缀AB是重合的, 也就是AB既是ABAB...的proper prefix又是其proper suffix. 定义Border[k], 每一个位置计算了前缀pattern[...k]的最长的重叠前后缀r的宽度: $$r = x_0, …, x_{i-1} = x_{k-i}, …, x_{k-1}$, 其中$i \in \{0, …, k-1 \}$$

比如abacab的border是ε和ab. ε的宽度为0.

在预处理阶段，确定pattern每个前缀的最宽border的宽度。然后在搜索阶段，可以根据已匹配的前缀来计算移位距离。

首先要知道border的性质:

Let r, s be borders of a string x, where |r| < |s|. Then r is a border of s. If s is the widest border of x, the next-widest border r of x is obtained as the widest border of s etc.

使用指针i指定pat前缀和指针j指向候选border, 如果pat[i] = pat[j], 那么border[i]就能扩展至j, 也就是border[i] = j

   j        i
   ↓        ↓
---# ... ---?
   ↑        
  b[i]

当出现不匹配时, 通过border的递归特性选择更小的border, 逐个尝试. 比如$\pi^{*}[5] = \{3, 1, 0 \}$.

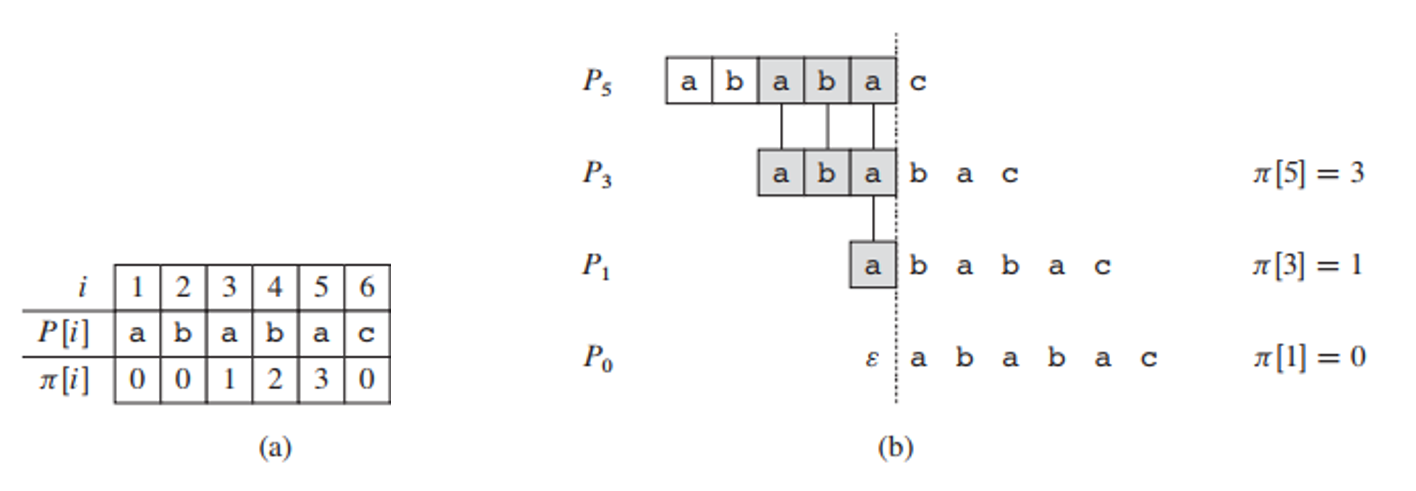
int[] border(String pat) {
	int i = 0, j = -1, m = pat.length();
	int[] b = new int[m + 1];
	b[i] = j;
	while (i < m) {
		while (j >= 0 && pat.charAt(i) != pat.charAt(j)) 
			j = b[j];
		i++; j++;
		b[i] = j;
	}
	return b;
}

running time $\Theta(m)$

nfa具象化为border数组, 在匹配时, 对齐移位距离由p已经匹配的前缀的最宽border来确定。

匹配

如果把上述预处理算法应用于字符串pt = pattern + text, 如果pt的某个前缀x有宽为m = len(pattern)的border, 则意味着有匹配. 这样就得出类似上面预处理算法的匹配算法.

int borderSearch(String txt, String pat, int[] border) 
{
	int i = 0, j = 0, n = txt.length(), m = pat.length();
	while (i < n) {
		while (j >= 0 && txt.charAt(i) != pat.charAt(j)) 
			j = border[j];
		i++;
		j++;
		if (j == m)
		{
			return i-j;
			// j = border[j]; // continue searching
		}
	}
	return -1;
}

Running time: at most N character accesses to Simulate NFA on text.

内部的while循环中, 如果在位置j处发生不匹配，则考虑pattern长度j的已匹配前缀的最宽border。根据border宽度b[j]对齐偏移继续匹配。如果再次发生不匹配，则考虑下一个最宽的border，依此类推，直到匹配或没有边界（j = -1）为止。

一个实例#

自动机匹配字符#

DFA KMP#

构建DFA#

NFA KMP#

Border#

匹配#

Reference#