字符搜索匹配算法 02 - Boyer-Moore(BM), Horspool, Sunday algorithms

Boyer-Moore算法

在从头到尾对齐txt的字符时, 每一次对齐, BM算法反方向从尾到头检查patternP=BAABBAA和txt字符是否匹配。匹配过程中如果发现txt[i] != P[j], 也就说二者子串不相等, 如...XAA != ...BAA, 且字符txt[i] = X在P中不存在时，可以把P开头对齐到txt[i+7], 一次就跳过了7个位置.

模式相较于文本一般较短, 所以模式中包含的字符种类相对也比较少, 那么这样的跳跃出现情况就很可观了, 可以大大加速匹配.

不过一般来说, 可能txt的某些子串会和P的其他子串重合，不失一般性我们需要像Knuth-Morris-Pratt算法一样的重启位置数组。

Bad Character Heuristic(BCH)

重启点位: 预先计算各个字符c在Pattern的最rightmost的位置(若无则-1), 这些位置告诉我们如果是txt中的字符c导致不匹配, pattern可以右移的距离.

badCharacterPreprocess(String pat)
{   // Compute skip table.
    this.pat = pat;
    int M = pat.length();
    int R = 256;
    right = new int[R];
    for (int c = 0; c < R; c++)
        right[c] = -1;            // -1 for chars not in pattern
    for (int j = 0; j < M; j++)   // rightmost position for
        right[pat.charAt(j)] = j; // chars in pattern
}

有了right数组后, 一个例子说明匹配过程:

     i   
txt: ...TLE...
P:   NEEDLE
         NEEDLE
        j

在匹配时如果发现字符不匹配txt[i+j] != P[j]，分三种情况考虑:

Mismatch character T not in pattern: increment i one character beyond T, i += j+1.
Mismatch character in pattern: mismatch character N in pattern, align text N with rightmost pattern N, i += j - right[N], 此时不会导致回退.
Mismatch character in pattern (but heuristic no help): mismatch character E in pattern, align text E with rightmost pattern E ? 此时会导致回退, 也就说j - right[E] < 0, 这种情况就直接i += 1.

public int search(String txt)
{   // Search for pattern in txt.
    int N = txt.length();
    int M = pat.length();
    int skip;
    for (int i = 0; i <= N-M; i += skip)
    {   // Does the pattern match the text at position i ?
        skip = 0;
        for (int j = M-1; j >= 0; j--)
        {
            if (pat.charAt(j) != txt.charAt(i+j))
            {
                skip = Math.max(1, j - right[txt.charAt(i+j)]);
                break;
            }
        }
        if (skip == 0) return i; // found.
    }
    return N;                    // not found.
}

Substring search with the Boyer-Moore bad character heuristic takes about ~ N / M character compares to search for a pattern of length M in a text of length N. Worst-case can be as bad as ~ M N.

Good Suffix Heuristics(GSH)

通过类似KMP的Border特性来提高效率，可以将最坏情况改善为O(~3N)字符比较。只不过这里需要的映射关系是一个已经匹配的border对应(包含在)pattern哪一个后缀中, 用shift[]数组记录. 对于pattern的一个后缀pat[j,...]的borderpat[j,...k] = pat[l, ...], 当不匹配时, 根据已匹配的borderpat[l, ...], 可以偏移l - k位置以对齐到pat[j,...k]. 当完成一个完整匹配后, GSH方法可以基于shift[]决定下一次对齐偏移的距离. 除此之外, 在匹配中如果发现不匹配字符, pattern的偏移距离可以在GSH和BCH给出的建议距离中选择最大者.

border: A border is a substring which is both proper suffix and proper prefix

Case 1. P有子串和后缀ab重复, 对齐重复的子串

0 1 2 3 4 5 6 7 8 9 ...
a b a a b a b a c b a
c a b a b
    c a b a b

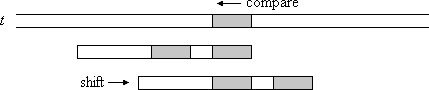
Case 2. P没有子串和后缀bab重叠, 但P的前缀ab与t的后缀ab匹配

0 1 2 3 4 5 6 7 8 9 ...
a a b a b a b a c b a
a b b a b      
      a b b a b

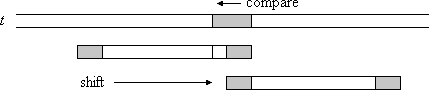
Case 3. P没有重复子串, 可以跳过整个P的长度

0 1 2 3 4 5 6 7 8 9 ...
a b c a b a b a c b a
c b a a b
          c b a a b

对于Case 1, 预处理时使用一个保存border position的数组bp, 每个元素bp[i]都包含模式P中从索引i开始的后缀的最宽border起始位置, 所以bp元素永远指向其右边的某一个位置。与Knuth-Morris-Pratt预处理算法相似，每个border都是通过检查是否匹配来向左扩展已知的较短边界来计算的。

当边界不能向左扩展时, 那就意味着在发生不匹配时, 可以把左边的border偏移过来。相应的偏移距离j - i保存在数组shift[j]中，前提是对应位置尚未被占用, 如果已经有占用(shift[i] != 0), 则意味着较短的后缀具有相同border的情况; 然后让border指针j跳转到bp[j], 因为bp[j]存下来之前计算的pat[j,...]的border, 同时我们知道pat[i] == pat[j], 这样保证了pat[i...]和pat[j...]有共同的前缀. 如此这般直到j > m. shift数组的值仅由那些无法扩增的border决定, 因为如果可以扩增的话, 意味着pat[i-1] = pat[j-1] != txt[k-1], 此时按照j - i来移位不过是继续出现不匹配.

i: 0 1 2 3 4 5 6 7
p: a b b a b a b 
b: 5 6 4 5 6 7 7 8
s: 0 0 0 0 2 0 4 1

如bp[2] = 4代表后缀babab的最宽border是以4起始的后缀bab. 因为pat[4-1] != pat[2-1], bab作为babab的border无法通过a扩增为b+babab的border, 因此shift[4] = 4 - 2.

注意到babab也有borderb, 无法扩增, 所以shift[6] = 6 - 2. 匹配时, 如果在匹配了pat[6...]后, pat[5]不匹配, 那么就可以偏移shift[6] = 4, 把pat[2]对齐过去.

匹配时在位置j发生任何不匹配时，就将模式对齐位置向右移动shift[j + 1]。

void goodSuffixPreprocessCase1(String pat) {
    int m = pat.length();
    int[] shift = new int[m + 1];
    int[] bp = new int[m + 1];
    int i = m;
    int j = m + 1;
    bp[i] = j;
    while (i > 0) {
        while (j <= m && pat.charAt(i - 1) != pat.charAt(j - 1)) {
            // could not extend border left forward
            if (shift[j] == 0) // prevent modification of shift[j] from suffix having same border
                shift[j] = j - i; // shift to i position
            j = bp[j]; // back to last border
        }
        i--; j--; // pat[i-1] == pat[j-1], extend border
        bp[i] = j;
    }
}

对于case 2，部分匹配的前缀是属于整个pattern的其中一个border(不一定是最大的). 预处理阶段，就是要计算pattern的每个后缀所包含的最大border, 同时要求这个border也必须属于整个pattern的border(也就是必须是pattern的前缀)。

因为case 1已经计算了pattern每个后缀的最大border，在这里考虑的是整个pattern, 其最大的border是b[0]. 首先把b[0]复制到shift[]的空位中(值等于0的位置); 然后对于长度比b[0]小的后缀pat[j...], 其一定不会包含后缀pat[b[0], ...], 所以需要替换为pattern下一个更小的border, j = bp[j].

i: 0 1 2 3 4 5 6 7
p: a b b a b a b
b: 5 6 4 5 6 7 7 8
s: 5 5 5 5 2 5 4 1

void goodSuffixPreprocessingCase2(String pat, int[] bp, int[] shift)
{
    int i, j = bp[0];
    for (i = 0; i <= m; i++)
    {
        if (shift[i] == 0) 
            shift[i] = j; // copy widest border
        if (i == j) // suffix becomes shorter than bp[0]
            j = bp[j]; 
    }
}

预处理汇总

以上三种预处理方式汇总在一起使用

bmPreprocess(String pat)
{
    badCharacterPreprocess();
    goodSuffixPreprocessingCase1();
    goodSuffixPreprocessingCase2();
}

匹配

从右到左比较pattern和txt的字符。

如果不匹配，pattern在BCH和GSH的偏移距离中选择较大者进行偏移对齐
如果完全匹配，pattern可以继续根据根据其最宽边框允许的数量移动。

void bmSearch(String txt, String pat)
{
    int i = 0; // shift of the pattern with respect to text
    int j;
    int m = pat.length(); 
    int n = txt.length(); 

    while (i <= n - m)
    {
        j = m - 1;
        while (j >= 0 && pat.charAt(j) == txt.charAt(i+j))
            j--; // reduce index if match with shift i
        if (j < 0) // complete matched
        {
            // return i; match 
            i += shift[0];
        }
        else // pat[i] != txt[i+j], shift shift[j+1]
            i += Math.max(shift[j+1], j - right[txt.charAt(i+j)]);
    }
}

Horspool Algorithm

BM算法使用BCH和GSH两种heuristics来决定shift距离. 不过GSH的实现非常复杂，而且在实践中发现，一般的字符集上的匹配性能主要依靠BCH。Horspool [Hor 1980] 提出了仅基于BCH的简化版BM方法: 不匹配时, 用当前查看的txt窗口的最右字符来确定shift距离。

(a) Boyer-Moore

0 1 2 3 4 5 6 7 8 9 ...
a b c a b d a a c b a
b c a a b
  b c a a b

(b) Horspool

0 1 2 3 4 5 6 7 8 9 ...
a b c a b d a a c b a
b c a a b
        b c a a b

Horspool使用当前txt窗口txt[0, ... 4]的最右边字符b作为判断, 把pattern[..., m-1]最右边的b(该字符在pattern最后位置的出现不计算在内)对齐到txt[4]。

预处理阶段会跟BM算法的BCH不一样, 对每一个字符$\alpha \in alphabet$, $right(pattern, \alpha)$ 取α在pattern[:-2]最右出现位置(如果没有则-1). 不考虑pattern[-1]. 如right['text', 'x'] = 2, right['text', 't'] = 0, right['next', 't'] = -1.

horspoolBCH(String pat)
{   // Compute skip table.
    this.pat = pat;
    int m = pat.length();
    int R = 256;
    right = new int[R];
    for (int c = 0; c < R; c++)
        right[c] = -1;            // -1 for chars not in pattern
    for (int j = 0; j < m - 1; j++)   // rightmost position for
        right[pat.charAt(j)] = j; // chars in pattern
}

匹配的过程和BM算法差不多。在完全匹配后或者遇到不匹配时，pattern就根据right[]数组移位

horspoolSearch(String txt, String pat, int[] right)
{
    int i = 0, j;
    while (i <= n - m)
    {
        j = m - 1;
        while (j >= 0 && pat.charAt(j) == txt.charAt(i+j)) 
            j--;
        if (j < 0)
            return i; // match
        i += m - 1; // right most of txt window
        i -= right[txt.charAt(i)];
    }
}

Sunday Algorithm

BM算法利用当前位置是否匹配来判断移位. Horspool利用当前检查的文本窗口内的最右字符来判断移位. Daniel M.Sunday [Sun 90] 发现如果能利用当前文本窗口外右边的字符更好, 考虑到这些字符有可能属于下一次可能的匹配, 这种思路是可行的.

0 1 2 3 4 5 6 7 8 9 ...
a b c a b d a a c b a
b c a a b
            b c a a b

不匹配时, Sunay算法利用当前文本窗口txt[0, ... 4]右边的字符, 也就是txt[5] = d来判断, d不再pattern中出现过, 因此直接跳过txt[5].

每次匹配都会从目标字符串中提取待匹配字符串与模式串进行匹配：

若匹配，则返回当前 idx
不匹配，则查看待匹配字符串的后一位字符 c：
- 若c存在于Pattern中，则 idx = idx + shift[c]
- 否则，idx = idx + len(pattern)
Repeat Loop 直到 idx + len(pattern) > len(String)

Shift偏移表

存储每一个在模式串中出现的字符，在模式串中出现的最右位置到尾部的距离 +1.

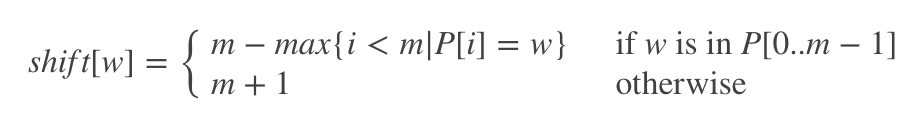
c h e c k t h i s o u t
t h i s
        |
          t h i s

m i s s i s s i p p i
i s s i 
        |
  i s s i

最坏情况：O(nm)

平均情况：O(n)

预处理阶段和horspool一样, 不过right的定义要改为在整个pattern[:]上求最右出现位置.

sundayBCH(String pat)
{   // Compute skip table.
    this.pat = pat;
    int m = pat.length();
    int R = 256;
    right = new int[R];
    for (int c = 0; c < R; c++)
        right[c] = -1;            // -1 for chars not in pattern
    //***********************************************************************
    for (int j = 0; j < m; j++)   // rightmost position for the whole pattern
    //***********************************************************************
        right[pat.charAt(j)] = j; // chars in pattern
}

sundaySearch(String txt, String pat, int[] right)
{
    int i = 0, j;
    while (i <= n - m)
    {
        /** matching from right to left
         * ********************************* **/
        j = m - 1;
        while (j >= 0 && pat.charAt(j) == txt.charAt(i+j)) 
            j--;
        if (j < 0)
            return i; // match
        /***********************************/

        i += m; // right next to txt window
        if (i < n) i -= right[txt.charAt(i)];
    }
    return -1;
}

因为Sunday算法不限定一定要从右往左对比pattern和txt, 反方向也行, 在这里的实现选择跟随Horspool算法从右往左.

Sunday 算法通常用作一般情况下实现最简单而且平均表现最好之一的实用算法，通常表现比 Horspool、BM 都要快一点。

可以在这里测试各种匹配算法的正确性和效率 https://leetcode-cn.com/problems/implement-strstr/

Reference

Boyer, RS and Moore, JS. “A fast string searching algorithm.” Communications of the ACM 20.10 (1977): 762-772.
R.N. Horspool: Practical Fast Searching in Strings. Software - Practice and Experience 10, 501-506 (1980)
D.M. Sunday: A Very Fast Substring Search Algorithm. Communications of the ACM, 33, 8, 132-142 (1990)
https://www.inf.hs-flensburg.de/lang/algorithmen/pattern/bmen.htm
https://www.inf.hs-flensburg.de/lang/algorithmen/pattern/horsen.htm
https://www.inf.hs-flensburg.de/lang/algorithmen/pattern/sundayen.htm
http://www-igm.univ-mlv.fr/~lecroq/string/

Boyer-Moore算法#

Bad Character Heuristic(BCH)#

Good Suffix Heuristics(GSH)#

预处理汇总#

匹配#

Horspool Algorithm#

Sunday Algorithm#

Shift偏移表#

Reference#