字符搜索匹配算法 03 Rabin-Karp Fingerprint & 字符串哈希

Rabin-Karp Fingerprint

Rabin-Karp fingerprint(RK) 基于 modular hashing：

Compute a hash of pattern characters 0 to M - 1.
For each i, compute a hash of text characters i to M + i - 1.
If pattern hash = text substring hash, check for a match.

如果在一一比较中对text的每个子串都重新计算hash，那么速度比暴力算法还慢。

所以算法的关键在于如何高效地计算哈希值：Horner’s method - M阶多项式hash的线性时间方法

$$a^b \pmod c = (a \pmod c)^b$$ 引理： $$(a \times b) \pmod c = [( a \pmod c ) \times (b \pmod c) ] \pmod c$$

即积的取余等于取余的积的取余.

根据modulars算术的基本性质，在每个算术运算后除以$Q$取余数，和执行完所有算术运算后再取除以Q的余数的结果一样。比如加法 $a+b = c$, then $a\pmod N+b\pmod N \equiv c$. 其中$\equiv$表示Congruence, 即$15 \equiv -9\pmod{12}$表示$15$和$9$对$12$取余的余数相同. 同理

If $a\equiv b\pmod N$, then $a+k \equiv b+k \pmod N$ for any integer $k$.
If $a\equiv b\pmod N$, and $c\equiv d\pmod N$, then $a+c \equiv b+d \pmod N$.
If $a \equiv b\pmod N$, then $-a \equiv -b\pmod N$.

乘法运算的取余满足:

If $a \cdot b = c$, then $a\pmod N\cdot b\pmod N \equiv c \pmod{N}$.
If $a \equiv b \pmod{N}$, then $ka \equiv kb \pmod{N}$ for any integer $k$.
If $a \equiv b \pmod{N}$ and $c \equiv d \pmod{N}$, then $ac \equiv bd \pmod{N}$.

Exponentiation:

If $a\equiv b\pmod{N}$, then $a^k \equiv b^k \pmod{N}$ for any positive integer kk.

使用多项式 Hash 计算pattern的hash，$h(d) = \Sigma d_i \times b^i \pmod Q$：

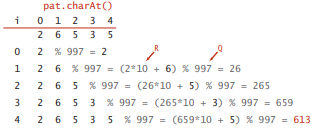
// Compute hash for M-digit key
private long hash(String key, int M)
{
    long h = 0;
    for (int j = 0; j < M; j++)
        h = (R * h + key.charAt(j)) % Q;
    return h;
}

RK算法的核心是，在pattern和text的对比中，如何动态地利用前面位置i已计算的值来计算新位置i+1的哈希. 给定$x_i$，如何计算$x_{i+1}$： $$x_i = t_i R^{M-1} + T_{i+1}R^{M-2} + … + t_{i+M-1}R^0$$ 其中M-digit, base-R integer, modulo Q $$x_{i+1} = t_{i+1}R^{M-1} + T_{i+2}R^{M-2} + … + t_{i+M}R^0$$ $$x_{i+1} = (x_i - t_i R^{M-1}) R + t_{i+M}$$

根据这个关系可知, 我们不必动态维护$x_i$值，而只需维护其除$Q$的余数即可。而且，$R^{M-1}$是可以预先计算的.

同时为了避免出现负数, 需要在每次运算中加一次Q(不影响取余结果) $$\begin{equation} \begin{aligned} (x_i + 1) \pmod Q &= (x_i + Q - t_i \times RM) \pmod Q \ &= (x_i - t_i \times RM) \pmod Q + (t_i \times Q) \pmod Q \end{aligned} \end{equation} $$

于是得出具体的搜索方法

public class RabinKarp
{
    private String pat; // pattern (only needed for Las Vegas)
    private long patHash; // pattern hash value
    private int M; // pattern length
    private long Q; // a large prime
    private int R = 256; // alphabet size
    private long RM; // R^(M-1) % Q
    
    public RabinKarp(String pat)
    {
        this.pat = pat; // save pattern (only needed for Las Vegas)
        this.M = pat.length();
        Q = longRandomPrime(); // See Exercise 5.3.33.
        RM = 1;
        for (int i = 1; i <= M-1; i++) // Compute R^(M-1) % Q for use
            RM = (R * RM) % Q; // in removing leading digit.
        patHash = hash(pat, M);
    }

    /** check for hash collision using rolling hash function */
    public int search(String txt)
    { // Search for hash match in text.
        int N = txt.length();
        long txtHash = hash(txt, M);
        if (patHash == txtHash) return 0; // Match at beginning.
        for (int i = M; i < N; i++)
        { // Remove leading digit, add trailing digit, check for match.
            txtHash = (txtHash + Q - RM*txt.charAt(i-M) % Q) % Q;
            txtHash = (txtHash*R + txt.charAt(i)) % Q;
            if (patHash == txtHash)
                if (check(i - M + 1)) return i - M + 1; // match
        }
        return N; // no match found
    }
}

Monte Carlo Correctness

存在哈希冲突, 如果要保证100%的字符匹配准确, 需要在hash匹配后, 进行一次字符的比对, 这就是Las Vegas版本的RK算法。而Monte Carlo版本的RK算法通过把映射hash表的Q值取尽可能大(比如long值$10^{20}$), 使得hash冲突概率降得尽可能低(如低至$1/Q = 10^{-20}$).

boolean check(int i) // Monte Carlo (See text.)
{ return true; } // For Las Vegas, check pat vs txt(i..i-M+1).

二者对比:

Monte Carlo version. Return match if hash match. Always runs in linear time. Extremely likely to return correct answer (but not always!).
Las Vegas version. Check for substring match if hash match; continue search if false collision.Always returns correct answer. Extremely likely to run in linear time (but worst case is M N).

In theory, if Q is a sufficiently large random prime (about $M N^2$), then the probability of a false collision is about 1 / N. In practice, choose Q to be a large prime (but not so large to cause overflow). Under reasonable assumptions, probability of a collision is about 1 / Q.

最长回文子串

字符串哈希还可以用于计算判断最长回文子串，需要分别预处理正着和倒着的哈希值; 判断是否可行时枚举回文中心（对称轴），哈希判断两侧是否相等。

总结

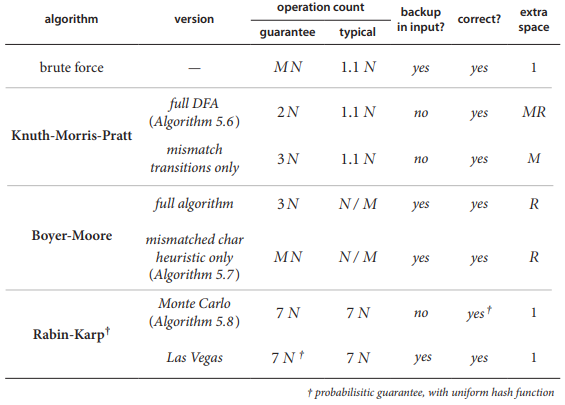算法可以拓展到二维模式匹配, 多模式匹配等问题.

Rabin-Karp Fingerprint#

Monte Carlo Correctness#

最长回文子串#

总结#

Rabin-Karp Fingerprint

Monte Carlo Correctness

最长回文子串

总结