循环神经网络

当人类阅读时，会根据对之前单词的理解和记忆来辅助理解当前看到的每个单词。也就是人能够很好地处理语言的长距离依赖特性（long-term dependency）。在自然语言处理任务中，很多传统的模型无法做到这一点，比如前馈神经网络；而传统的n-gram模型固然可以通过把把n系数增大来捕捉长距离依赖，但带来的非常巨大的内存消耗。

循环神经网络（Recurrent Neural Networks, RNNs)可以看做是多个共享参数的前馈神经网络不断叠加的结果 ![](http://colah.github.io/posts/2015-08-Understanding-LSTMs/img/RNN-unrolled.png “A recurrent neural network and the unfolding in time of the computation involved in its forward computation. “image from: http://colah.github.io”)

这里的核心是想办法解码历史信息, 即通过递归方程$s_i = R(x_i, s_{i−1})$让$s_i$解码序列$x_{1:n}$. 比如把所有历史信息累加就是一种非常简单粗暴的方式, 这样得到的是连续词袋模型(continuous-bag-of-words model)$s_i = R_{CBOW}(x_i, s_{i-1}) = x_i + s_{i−1}$, 虽然简单，但这种RNN其实忽略了数据的时序性质。

一般意义上的RNN是指Elman Network or Simple-RNN (S-RNN)(Elman [1990]), $s_i = R_{SRNN}(x_i, s_{i-1}) = g(x_iW^x + s_{i−1}W^s + b)$, 也就是把历史信息先进行线性变换(乘以矩阵), 再和bias加起来, 再通过一个非线性激活函数(tanh或ReLU). 添加了线性变换再进行非线性激活, 使网络对输入的顺序变得敏感。

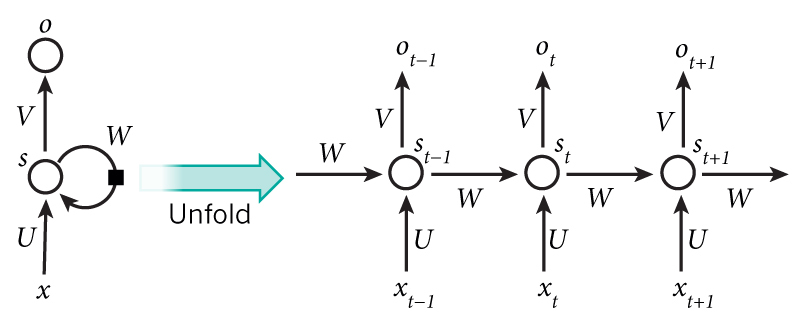在使用时, 给定输入序列（单词序列或语音）得出输出序列的过程如下：

  • 把每个词$x_{t}$(以向量表示)逐个输入RNN
  • 每一时间步$t$都有对应的隐含状态$s_t$，用于解码历史信息: $s_t = g(Ux_t + Ws_{t-1} + b)$.
  • 每一时间步都可以有一个输出（虽然大部分应用只用到最后一时间步）$o(t)$： 例如，语言模型想要预测下一个单词，那么输出就是在词汇表上的概率分布向量，$o_t = softmax(Vs_t)$.
  • 其中，各个时间步共享几个参数矩阵（$U, V, W$）

In addition to the above normal many to many structure RNNs, there are other non-sequence input or output: Many to one, e.g. when predicting the sentiment of a sentence we may only care about the final output, not the sentiment after each word. One to many: Music generation.

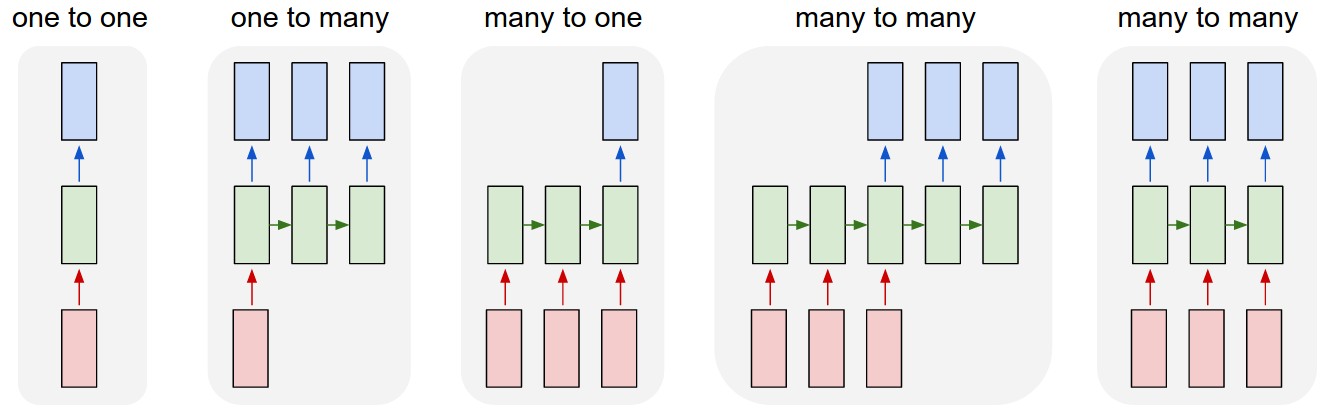
除了应用于语言模型, RNNs 还可以应用于 · tagging, e.g. part-of-speech tagging, named entity recognition (many to many RNNs) · sentence classification, e.g. sentiment classification (many to one RNNs) · generate text, e.g. speech recognition, machine translation, summarization

RNNs Backpropagation

Backpropagation Through Time (BPTT): Because the parameters are shared by all time steps in the network, the gradient at each output depends not only on the calculations of the current time step, but also the previous time steps.

RNNs trained with BPTT have difficulties learning long-term dependencies (e.g. dependencies between steps that are far apart) due to what is called the vanishing/exploding gradient problem.

梯度消失与爆炸

The Vanishing/Exploding Gradient problem。

RNNs shares the same matrix (w, u, etc.) at each time step during forward prop and backprop. 求导数时, 根据链式法则, loss对各参数的导数会转换为loss对输出y的导数, 乘以y对隐含层的导数, 乘以隐含层相对隐含层之间的导数, 再乘以隐含层对参数的导数.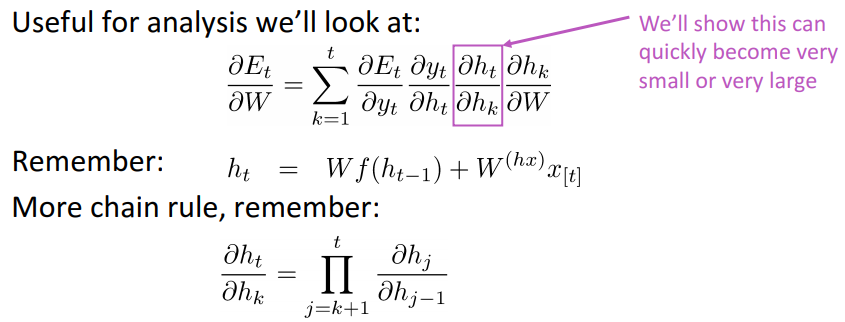

不同隐含层（举例如$h_t$和$h_k$）之间如果相隔太远, $h_t$对$h_k$的导数就变成多个jacobian矩阵的相乘， 对各个jacobian范数（norms）进行分析后，发现$h_t$对$h_k$的导数值在训练过程中会很快变得很极端（非常小或者非常大）。

Gradient作为传导误差以帮助系统纠正参数的关键角色，如果本身变得接近于0或者nan，那么我们就无法判断t和t+n的数据的依赖性（是没有依赖？还是因为vanish of gradient？还是因为参数设置错误？）。梯度衰减会直接降低模型学习长距离依赖关系的能力，给定一个时间序列，例如文本序列，循环神经网络较难捕捉两个时刻距离较大的文本元素（字或词）之间的依赖关系。

在使用RNN学习language model的时候，非常容易出现梯度爆炸，解决办法是使用 gradient clipping 梯度裁剪，就是通过把梯度映射到另一个大小的空间，以限制梯度范数的最大值On the difficulty of training Recurrent Neural Networks。

虽然梯度裁剪可以应对梯度爆炸，但无法解决梯度衰减的问题。一个缓解梯度衰减的方案是使用更好的参数初始化方案和激活函数（ReLUs）A Simple Way to Initialize Recurrent Networks of Rectified Linear Units.

不过更主流的解决梯度衰减的方案是使用更复杂的rnn隐含单元: Gated Recurrent Units (GRU) introduced by Learning Phrase Representations using RNN Encoder-Decoder for Statistical Machine Translation and LSTMs.

门控循环网络

因为梯度消失的问题，RNN的解码能力是很有限的。S-RNN架构的一个明显缺陷是对历史信息的记忆是不受控制，在每一时间步的计算，读写整个记忆状态$s_t$。而门控循环网络，比如Long Short-Term Memory（LSTMs），Gated Recurring Unit（GRUs），使用门的概念，让网络拥有控制哪些信息需要记录, 哪些需要丢弃的能力。如何实现这种门呢? 考虑一种介于[0, 1]中间的因子, 让这种因子与各种状态信息相乘, 可以为每个状态信息独自训练一个因子, 也就是由简单的神经网络(非线性激活函数Sigmoid)来控制.

是否允许信息通过（打开）或不通过（关闭）取决于其门控单元内部Sigmoid激活层的点乘运算。Sigmoid函数值介于0和1之间，可用于描述允许通过单元格的信息量。

LSTM架构将状态向量$s_i$分成两半，其中一半被视为“记忆单元”$C$, 而另一半被视为一般的工作存储单元-隐含状态$h$。

1, LSTM用遗忘门来决定从前一时间步的记忆单元中丢弃哪些信息，控制当前记忆单元应该忘记多少来自前一步状态$h_{t-1}$的信息量，标记为遗忘信息。遗忘门由一个sigmoid层学习而来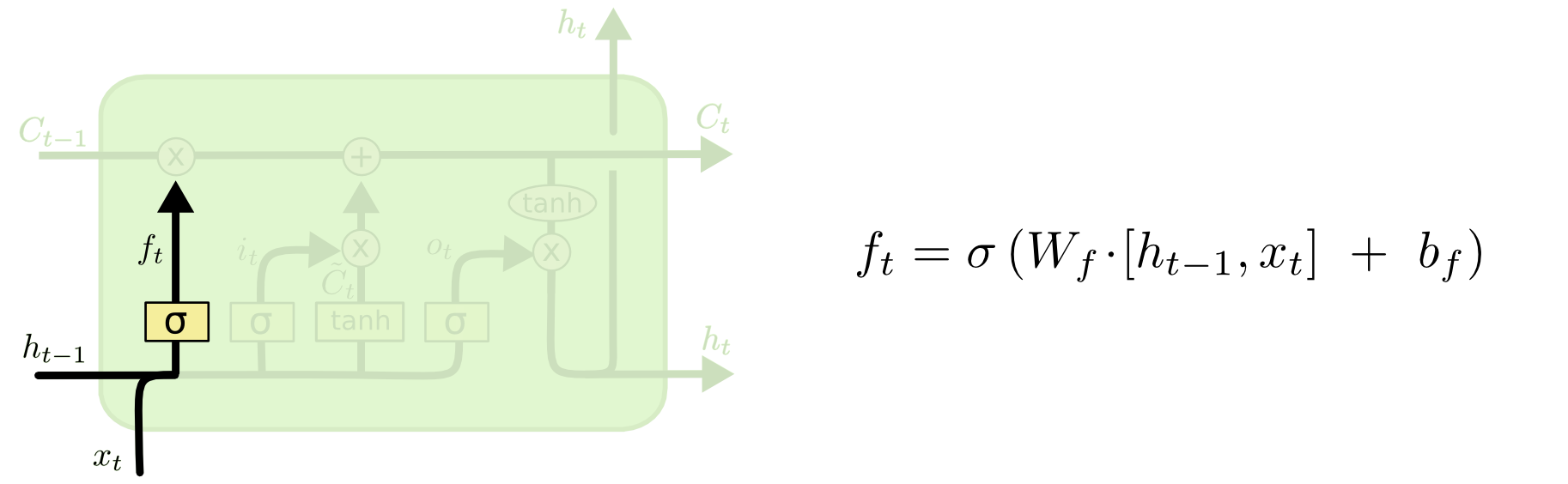

2, 用输入门 Input gate (a sigmoid hidden layer) 来决定有多少新信息是值得储存的（当前时间步$t$）。输入门控制哪些信息需要更新. 再通过一个隐含层(tanh/relu)生成新的候选信息向量$\widetilde{C}_t$.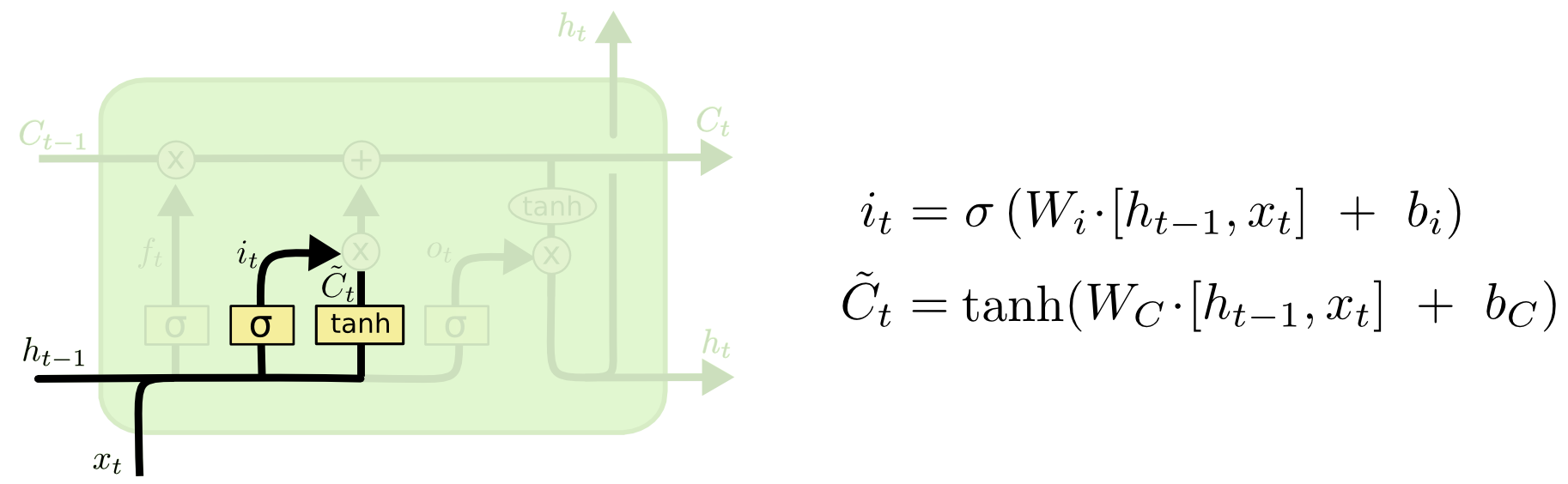

输入门和遗忘门一起，控制每一步的信息存储和改写, 将遗忘信息和候选信息组合在一起作为更新信息，作为当前时间步的新记忆单元，$C_{t}$.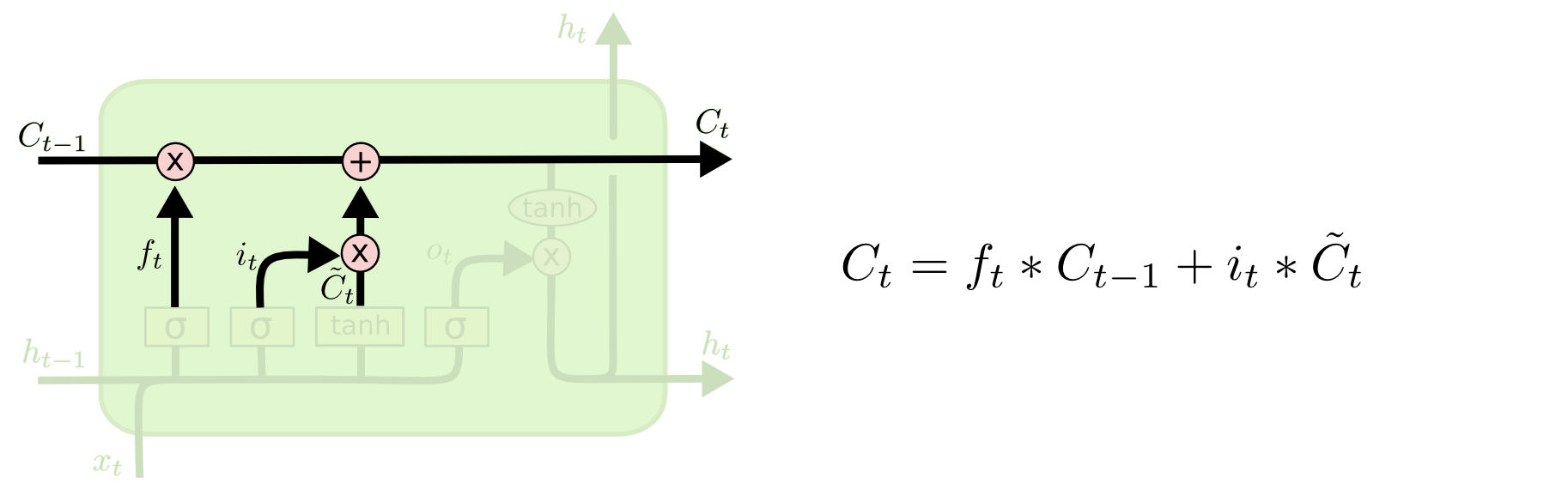

3, 最后，用一个输出门 Output gate (a sigmoid layer) 来控制多少记忆单元作为当前步的工作隐含状态$h_t$。先通过一个tanh激活层把当前记忆单元$C_t$推送为[-1, 1]之间的值, 再乘以输出门.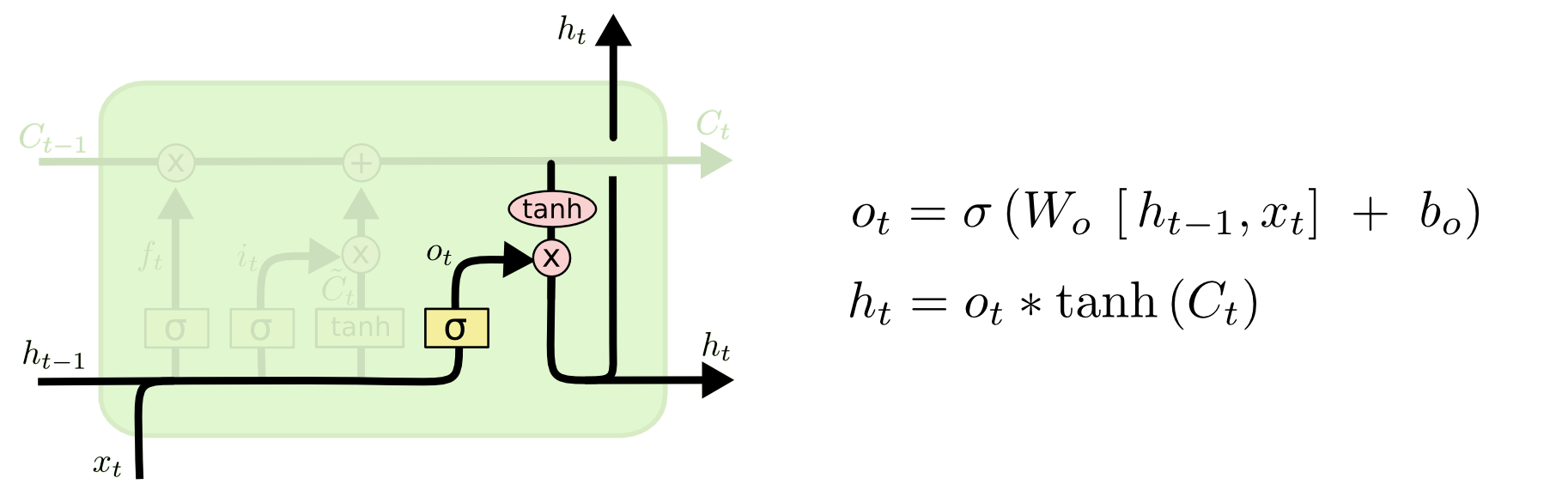

总的来说, LSTM有遗忘门, 输入门和输出门这三个门. 加上其中的更新信息, 形式上LSTM有四个神经网络, 输入都是上一步隐含状态和当前步的输入向量的.

GRUs

LSTMs分别使用记忆单元和隐含状态来控制信息流, 其中最新的隐含状态需要用到最新的记忆单元来计算，每一步输出只用到隐含状态的信息，也就说记忆单元本质上是为隐含状态的更新服务的。而记忆单元自身就用到了三个神经网络来计算，而且可以看到记忆单元和隐含状态的计算似乎有一些冗余。比如LSTM的遗忘门和更新门，更新和遗忘本身就是相伴相随的，对于一个记忆单元来说，本身的容量是固定的，需要更新多少信息，自然也意味着需要遗忘多少信息，也就是可以用一个神经网络来控制。随着数据量的增大和神经网络增大，是否可以把一些门合并简化？

GRUs (Cho, et al. (2014))就抛弃了记忆单元的设定, 只用隐含状态 $h$ 来表达信息流. GRUs首先根据当前的输入词向量和隐含状态计算更新门$z_t$和一个重置门$r_t$。核心是更新门$z_t$，用于控制更新多少新的候选信息$\widetilde{h}t$, 同时意味着只保留$(1 - z_t)$的旧信息$h{t-1}$. 隐含状态的候选信息$\widetilde{h}_t$用重置门$r_t$计算.

LSTMs的遗忘门和输入门的合作核心是更新信息. 而GRUs将LSTMs的遗忘门和输入门合并成一个更新门, 抛弃了输出门的概念, 让更新门负责计算新的隐含状态. 这样GRUs内部总共只有两个门, 三个神经网络, 某种程度上简化了LSTMs模型。

GRU intuition

  • 重置门赋予了模型丢弃与未来无关的信息的能力。若重置门接近于0，则忽略之前的记忆，仅储存新加入的信息.
  • 更新门控制过去的状态对现在的影响程度（即决定更新多少），如果接近于$1$，则 $h_t=z_t\cdot h_{t-1}$, 等同于把过去的信息完整复制到未来，相应地缓解梯度衰减。
  • 短距离依赖的单元，过去的信息仅保留很短的时间，重置门一般很活跃，也就是数值在0和1之间频繁变动。
  • 长距离依赖的单元，重置门较稳定（保留过去的记忆较长时间），而更新门较活跃。

不同RNNs变种的比较

Vanilla RNNs Execution:

  1. Read the whole register h
  2. Update the whole register

GRU Execution:

  1. Select a readable subset
  2. Read the subset
  3. Select a writable subset
  4. Update the subset

门控循环神经网络的训练

  1. 把参数矩阵初始化为正交
  2. 把遗忘门的bias初始化为1，默认不遗忘
  3. 别忘了梯度裁剪
  4. 注意dropout在RNNs中的应用不同于DNN和CNN

Bidirectional RNNs

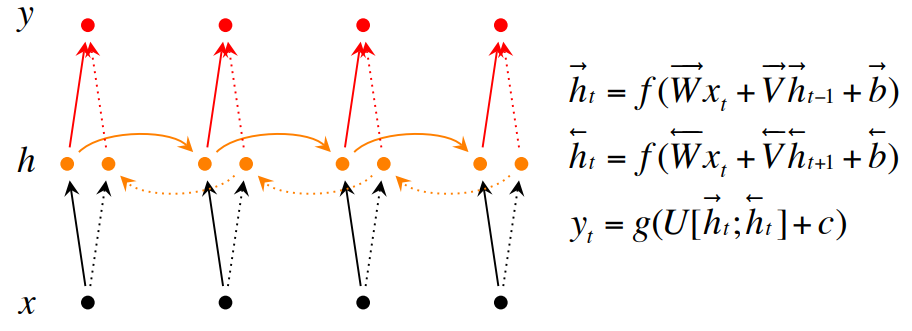
Bidirectional RNNs are based on the idea that the output at time t may not only depend on the previous elements in the sequence, but also future elements. They are just two RNNs stacked on top of each other. The output is then computed based on the hidden state of both RNNs.

参考资料

斯坦福cs224n http://web.stanford.edu/class/cs224n

http://colah.github.io

Neural Network Methods in Natural Language Processing, by Yoav Goldberg