序列标注（Sequence Labeling）

序列标注任务是指根据观察得到的序列（如一个句子）, 推断出序列每个元素（单词）对应的标注。

具体的任务包括分词(Segmentation), 词性标注（Part-of-Speach tagging, POS）, 实体识别(Named Entity Recognition, NER), 等等. 所谓POS, 就是对于一个句子, 如Bob drank coffee at Starbucks, 标注可能为Bob (NOUN) drank (VERB) coffee (NOUN) at (PREPOSITION) Starbucks (NOUN).

除此之外, 还有其他涉及到需要根据观察序列推断隐含状态的问题, 这种问题的特点是每一个位置的标签都不是独立的, 而是和上下文相关依存的, 可以用序列标注的思路来处理.

单个分类器仅能预测单个类变量，但是序列标注基于概率图模型, 图模型(Graphical Models)的真正功能在于它们能够对许多有相互依赖的变量进行建模。最简单的依赖关系可以描述为一种线性链(Linear Chain), 也就是后续介绍到的隐马尔可夫模型(Hidden Markov Model, HMM)用到的假设.

概率图模型

Graphical Models, 用图的形式表示随机变量之间条件依赖关系的概率模型，是概率论与图论的结合。图中的节点表示随机变量，缺少边表示条件独立假设。

G = (V, E). 其中 V: vertex, 顶点/节点, 表示随机变量. E: edge, 边/弧. 如果两个节点不存在边, 则二者条件独立. 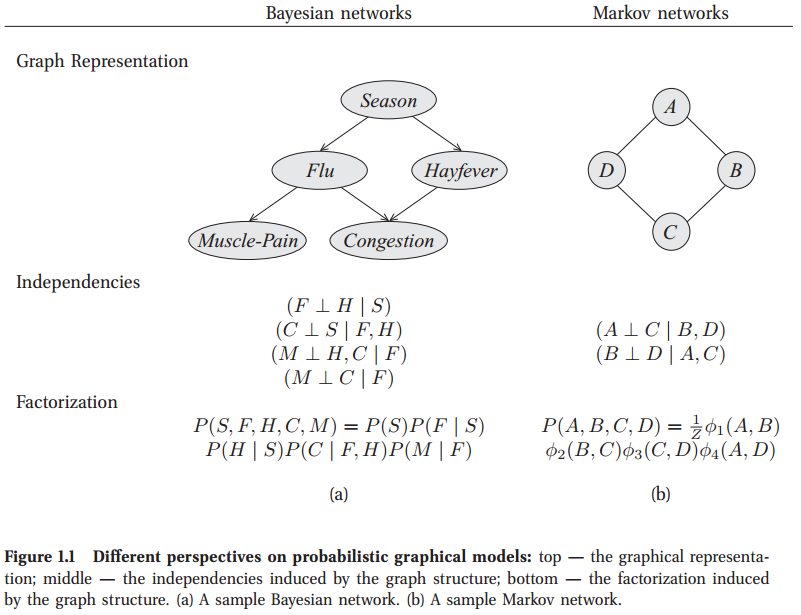从图上可以看到, 贝叶斯网络(Bayesian Networks, BNs)是有向图, 每个节点的条件概率分布表示为P(当前节点 | 父节点).

而马尔可夫网络则是无向图. 无向图形模型是指一整个家族的概率分布，每个概率分布都根据给定的因子集合进行因式分解。一般用random field来指代无向图中定义的特定分布. 数学上表达无向图, 指给定子集$\{Y_a \}_{a=1}^A$, 对于所有$\mathbf{y}_a$和任何因子选项$\mathcal{F}=\{\Psi_a\}$, $\Psi_a(\mathbf{y}_a) \geq 0$, 无向图定义的各个分布可以写成:

$$p(\mathbf{y})=\frac{1}{Z} \prod_{a=1}^A \Psi_{a}\left(\mathbf{y}_{a}\right)$$

Z是正则项用于保证分布$p$和为$1$ $$Z=\sum_{\mathbf{y}} \prod_{a=1}^{A} \Psi_{a}\left(\mathbf{y}_{a}\right)$$

Markov Net 包含了一组具有马尔可夫性质的随机变量. **马尔可夫随机场(Markov Random Fields, MRF)**是由参数$λ=(S, π, A)$表示, 其中S是状态的集合，π是初始状态的概率, A是状态间的转移概率。一阶马尔可夫链就是假设t时刻的状态只依赖于前一时刻的状态，与其他时刻的状态和观测无关。这个性质可以用于简化概率链的计算。使用类似性质作为假设的模型还有Bi-gram语言模型等.

朴素贝叶斯分类器与隐马尔可夫模型

朴素贝叶斯分类器(NBs)假设条件独立性(朴素贝叶斯假设, Hand and Yu, 2001)：$p(x_i | y, x_j) = p(x_i | y)$, 在给定目标值 y 时，x的属性值之间相互条件独立。这样, 计算可以简化为 $$p(y | \overrightarrow{x}) \propto p(y, \overrightarrow{x}) = p(y) \prod_{i=1} p(x_i | y).$$

朴素贝叶斯模型只考虑了单个输出变量y。如果要为一个观察序列$\overrightarrow{x} =(x_1, …, x_n)$预测对应的分类序列$\overrightarrow{y} =（y_1, …, y_n)$ ，一个简单的序列模型可以表示为多个NBs的乘积。此时不考虑序列单个位置之间的相互依赖。$$p(\overrightarrow{y}, \overrightarrow{x}) = \prod^n_{i=1} p(y_i) p(x_i | y_i).$$ 此时每个观察值$x_i$仅取决于对应序列位置的类变量$y_i$。由于这种独立性假设，从一个步骤到另一个步骤的转换概率不包括在该模型中。然而这种假设在实践中几乎不会符合，这导致这种模型的性能很有限。

因此，比较合理的假设是观测序列在连续相邻位置间的状态存在依赖。要模拟这种依赖关系, 就要引入状态转移概率$p(y_i | y_{i-1})$, 由此引出著名的隐马尔可夫模型 Hidden Markov model, HMM, Rabiner (1989).

HMM参数$λ = (Y, X, π, A, B)$ ，其中Y是隐状态（输出变量）的集合，X是观察值（输入）集合，π是初始状态的概率，A是状态转移概率矩阵$p(y_i | y_{i-1})$，B是输出观察值概率矩阵$p(x_i | y_{i})$。在POS任务中, X就是观察到的句子, Y就是待推导的标注序列, 因为词性待求的, 所以人们称之为隐含状态.

概括一下HMM设定的假设:

  1. Markov assumption：假设每个状态仅依赖于其前一个状态, $p(y_t|y_{t−1})$
  2. Stationarity assumption：状态的转换概率与转换发生的实际时间（实际输入）无关
  3. Output independence assumption: 假设每一个观察值x仅依赖于当前状态值y, $p(x_t|y_t)$, 而与前面的观察值无关。

那么状态序列y和观察序列x的联合概率可以分解为 $$p(\mathbf{y}, \mathbf{x})=\prod_{t=1}^{\mathrm{T}} p\left(y_{t} | y_{t-1}\right) p\left(x_{t} | y_{t}\right)$$

总的来说, 隐马尔可夫模型（HMM）是具有随机状态转移和观测值的有限状态自动机（Rabiner，1989）。自动机对概率生成过程进行建模: 先从某个初始状态开始，发射(emit)该状态生成的观察值，再转移到下一个状态，再发射另一个观察值，以此类推，直到达到指定的最终状态，从而产生一系列观察值。

HMM作为生成式的概率模型, 对观察特征的条件独立约束非常严格. 而且为了定义观察值序列和序列标记的联合概率，生成模型需要枚举所有可能的观察序列. 对于表示多个相互作用的特征或观测值的长距离相关性, 这种枚举是不切实际的，因为此类模型的inference很棘手。但很多任务往往受益于这种相互作用、相互交叉重叠的特征，比如除了传统的单词自身外，还有大小写，单词结尾，词性，格式，在页面上的位置以及WordNet中的节点成员身份等等。

除此之外, 大部分文本任务是根据给定的观察序列（如纯文本）来预测对应的状态序列，也就是判别问题。换句话说，HMM不恰当地用了生成联合概率的模型去判别问题。

隐马尔可夫模型与最大熵马尔可夫模型

最大熵马尔可夫模型(Maximum Entropy Markov Models, MEMM)跟HMM的生成式概率图不同，MEMM对当前状态的判断依赖于前一时间步的状态和当前观察值的状态。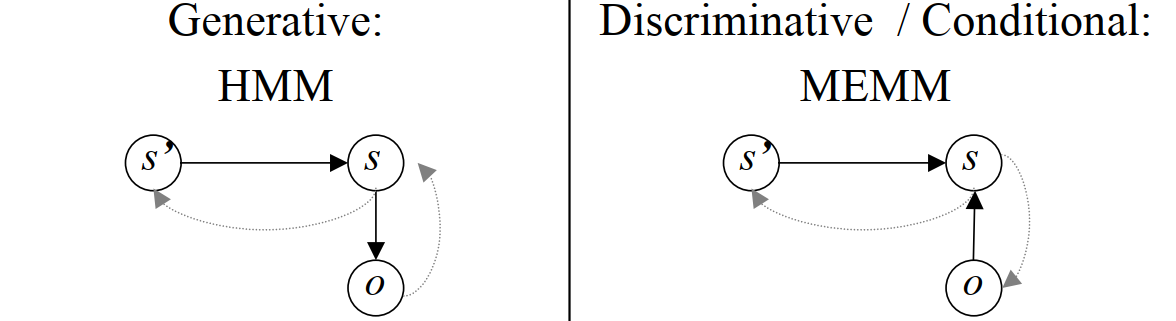

首先所谓"熵"就是信息论中的概念:

Entropy: the uncertainty of a distribution.

量化Entropy: surprise. Entropy = expected surprise

Event $x$, Probability $p_x$, “Surprise” $log(1/p_x)$, Entropy: $$ \begin{aligned} &H(p)=E_{p}\left[\log \frac{1}{p_{x}}\right]\ &\mathrm{H}(p)=-\sum_{x} p_{x} \log p_{x} \end{aligned} $$

熵最大的分布就是均匀分布，也就是每一个选项都一样，等于什么信息都没给。如果给了额外的信息，如约束，特征之后，熵就可以降低。

“最大熵”是指遵循最大熵原则：

model all that is known and assume nothing about that which is unknown.

也就说, 如果给定了一组事实，我们最好选择一个符合这些事实的模型，剩余情况则尽可能地一视同仁不做任何区别对待。最佳的模型是符合训练数据衍生的约束条件的模型，同时尽可能少地做假设，也就是少做承诺，也就避免过拟合。

MEMM 把HMM中的转移概率和发射概率替换为一个概率：当前状态$s$依赖于前一个状态$s^{\prime}$和当前观察值$o$, $\mathrm{P}\left(s | s^{\prime}, o\right)$

MEMM的训练思路是这样: 对每个状态$s^{\prime}$, 将训练数据分为<观察-目标状态>对 $<o, s>$, 也就是把 $\mathrm{P}\left(s | s^{\prime}, o\right)$ 分成 $|S|$ 个分别训练的exponential model $\mathrm{P}_{s^{\prime}}(s | o)=\mathrm{P}\left(s | s^{\prime}, o\right)$, 再通过最大化熵来训练exponential models, 换种说法叫logistic regression classifier.

用的约束条件是学习分布中每个特征$a$的期望值与训练数据的观测序列上每个特征的期望值相同. 满足这些约束的最大熵分布（Della Pietra，Della Pietra和Lafferty，1997）是唯一的，与最大似然分布一致，对每一个位置的状态$s^{\prime}$, 具有指数形式： $$ P_{s^{\prime}}(s | o)=\frac{1}{Z\left(o, s^{\prime}\right)} \exp \left(\sum_{a} \lambda_{a} f_{a}(o, s)\right) $$

其中$\lambda_{a}$是待估计的参数, $Z\left(o, s^{\prime}\right)$是归一化因子 $$ Z\left(o, s^{\prime}\right)=\sum_{s \in S} P\left(s | s^{\prime}, o\right) $$ $S$是标签集.

如果把问题简化为线性的相邻依赖, 那么每一个状态$s_{i}$仅依赖于前一个状态$s_{i-1}$. 用$Y$表达标签序列, 用$X$表达观察序列, 那么 $$P\left(y_{1}, y_{2}, \ldots, y_{n} | \mathbb{x}\right)=P\left(y_{1} | \mathbb{x}\right) P\left(y_{2} | \mathbb{x}, y_{1}\right) P\left(y_{3} | \mathbb{x}, y_{2}\right) \ldots P\left(y_{n} | \mathbb{x}, y_{n-1}\right)$$ 其中 $$P\left(y_{1} | \mathbb{x}\right)=\frac{e^{f\left(y_{1} ; \mathbb{x}\right)}}{\sum_{y_{1} \in S} e^{f\left(y_{k} ; \mathbb{x}\right)}}, \quad P\left(y_{k} | \mathbb{x}, y_{k-1}\right)=\frac{e^{g\left(y_{k-1}, y_{k}\right)+f\left(y_{k} ; \mathbb{x}\right)}}{\sum_{y_{k} \in S} e^{g\left(y_{k-1}, y_{k}\right)+f\left(y_{k} ; \mathbb{x}\right)}}$$ 则 $$P(\mathbb{y} | \mathbb{x})=\frac{e^{f\left(y_{1} ; \mathbb{x}\right)+g\left(y_{1}, y_{2}\right)+f\left(y_{2} ; \mathbb{x}\right)+\cdots+g\left(y_{n-1}, y_{n}\right)+f\left(y_{n} ; \mathbb{x}\right)}}{\left(\sum_{y_{1} \in S} e^{f\left(y_{1} ; \mathbb{x}\right)}\right)\left(\sum_{y_{2} \in S} e^{g\left(y_{1}, y_{2}\right)+f\left(y_{2} ; \mathbb{x}\right)}\right) \cdots\left(\sum_{y_{n} \in S} e^{g\left(y_{n-1}, y_{n}\right)+f\left(y_{n} ; \mathbb{x}\right)}\right)}$$ MEMM将整体的概率分布分解为每一个时间步的分布之积，所以算loss只需要把每一步的交叉熵求和。只需要每一步单独执行softmax，所以MEMM是完全可以并行的，速度跟直接逐步Softmax基本一样。

虽然MEMM能克服HMM的很多弱点, 但是MEMM自身也有一个 label bias 问题, 就是标签偏差, 离开给定状态的转移仅相互对比，而不是与全局所有其他转移对比。转移分数是分别对每个状态的归一化, 这意味到达一个状态的所有质量必须在可能的后续状态之间分配。观察值可以影响哪个目标状态获得质量，但无法影响多少质量可以被传递。这会导致模型偏向输出选择较少的状态, 比如极端情况下, 在训练集中某个状态$s_a$只发现了有一种可能的转移$s_b$, 那么状态$s_a$别无选择，只能将所有质量传递给它的唯一的 transition output $s_b$。

随机场

随机场, 可以看成是一组随机变量的集合（这组随机变量对应同一个样本空间）。当给每一个位置按照某种分布随机赋予一个值之后，其全体就叫做随机场。这些随机变量之间可能有依赖关系，一般来说，也只有当这些变量之间有依赖关系的时候，我们将其单独拿出来看成一个随机场才有实际意义。

如果给定的MRF中每个随机变量下面还有观察值，我们要确定的是给定观察集合下，这个MRF的分布，也就是条件分布，那么这个MRF就称为 Conditional random fields (CRF)。它的条件分布形式完全类似于MRF的分布形式，只不过多了一个观察集合X。所以, CRF本质上是给定了条件(观察值observations)集合的MRF.

1.特征函数的选择: 特征函数的选取直接关系模型的性能。 2.参数估计: 从已经标注好的训练数据集学习条件随机场模型的参数，即各特征函数的权重向量λ。 3.模型推断: 在给定条件随机场模型参数λ下，预测出最可能的状态序列。

MEMM和CRF

在CRF的序列标注问题中，我们要计算的是条件概率 $$ P\left(y_{1}, \ldots, y_{n} \mid \mathbb{x}\right), \quad \mathbb{x}=\left(x_{1}, \ldots, x_{n}\right) $$

CRF和MEMM的关键区别在于，MEMM使用每个状态的指数模型来确定给定当前状态的下一状态的条件概率，而CRF则使用一个指数模型来表示整个标签序列的联合概率, 这个概率条件依赖于给定的完整观察序列。二者区别仅在于分母（也就是归一化因子）的计算方式不同，CRF的是全局归一化的，而MEMM的是局部归一化的. 也就是说CRF是一个以观测序列$X$为全局条件的随机场. 存在函数$f(y_1,\dots,y_n;\mathbb{x})$，使得 $$ P(y_1,\dots,y_n|\mathbb{x})=\frac{1}{Z(\mathbb{x})}\exp\Big(f(y_1,\dots,y_n;\mathbb{x})\Big) $$

可以得到对应得概率是 $$P(\mathbb{y} | \mathbb{x})=\frac{e^{f\left(y_{1}, y_{2}, \ldots, y_{n} ; \mathbb{x}\right)}}{\sum_{y_{1}, y_{2}, \ldots, y_{n} \in S^n} e^{f\left(y_{1}, y_{2}, \ldots, y_{n} ; \mathbb{x}\right)}}$$ CRF的计算困难之处在于上式的分母项包含了所有可能路径$S^n$的求和，搜索空间非常庞大.

因此做出一些简化，假设输出之间的关联仅发生在相邻位置，并且关联是指数加性的:

$$\begin{aligned} f\left(y_{1}, y_{2}, \ldots, y_{n} ; \mathbb{x}\right) &=f\left(y_{1} ; \mathbb{x}\right)+g\left(y_{1}, y_{2};\mathbb{x}\right)+\cdots+g\left(y_{n-1}, y_{n};\mathbb{x}\right)+f\left(y_{n} ; \mathbb{x}\right) \\ &=f\left(y_{1} ; \mathbb{x}\right)+\sum_{k=2}^{n}\left(g\left(y_{k-1}, y_{k};\mathbb{x}\right)+f\left(y_{k} ; \mathbb{x}\right)\right) \end{aligned}\tag{1}$$

只需要对每一个标签和每一个相邻标签对分别打分，然后将所有打分结果求和得到总分。

Linear Chain CRF

尽管CRF已经做了一些简化假设，但一般来说，(1)式所表示的概率模型还是过于复杂，难以求解。于是考虑到当前深度学习模型中，RNN或者层叠CNN等模型已经能够比较充分捕捉各个$y$与输入$x$的联系，因此，我们不妨考虑函数$g$跟$x$无关，那么 $$\begin{aligned} f\left(y_{1}, y_{2}, \ldots, y_{n} ; \mathbb{x}\right) &=h\left(y_{1} ; \mathbb{x}\right)+g\left(y_{1}, y_{2}\right)+\cdots+g\left(y_{n-1}, y_{n}\right)+h\left(y_{n} ; \mathbb{x}\right) \\ &=h\left(y_{1} ; \mathbb{x}\right)+\sum_{k=2}^{n}\left(g\left(y_{k-1}, y_{k}\right)+h\left(y_{k} ; \mathbb{x}\right)\right) \end{aligned}$$ 其中$g\left(y_{k-1}, y_{k}\right)$是一个有限的、待训练的参数矩阵，而单标签的打分函数$h(y_i;\mathbb{x})$我们可以通过RNN或者CNN来建模。因此，该模型是可以建立的，其中概率分布变为 $$ P(y_1,\dots,y_n|\mathbb{x})=\frac{1}{Z(\mathbb{x})}\exp\left(h(y_1;\mathbb{x})+\sum_{k=1}^{n-1}\Big[g(y_k,y_{k+1})+h(y_{k+1};\mathbb{x})\Big]\right)\tag{2} $$

直接引用(Sutton, C. 2010)的定义:

在CRF中，首先需要定义特征函数.

然后为每个特征函数$f_{j}$分配权重$\lambda_j$, 权重是从数据中学习而来. 对$j$个特征方程求和, 对序列每个位置$i$求和:

$$ score(y | x) = \sum_{j = 1}^m \sum_{i = 1}^n \lambda_j f_j(s, i, y_i, y_{i-1})$$

CRF的每个特征函数都是一个输入的函数, 对应的输出是一个实数值（只是0或1）。例如, 选择特征函数$f_1(x, i, y_i, y_{i-1}) = 1$, 当且仅当$y_i = ADVERB$, 且第i个单词以“-ly”结尾; 否则为0. 如果与此特征相关的权重$\lambda_j$很大且为正，那么这个特征等同于说模型倾向于把以-ly结尾的单词标记为ADVERB。

通过指数化和归一化把这些得分转换为概率值: $$p(y | x) = \frac{exp\left(score(y|x)\right)}{\sum_{y^\prime} exp\left(score(y^\prime|x)\right)} = \frac{exp\left(\sum_{j = 1}^m \sum_{i = 1}^n \lambda_j f_j(x, i, y_i, y_{i-1})\right)}{\sum_{y^{\prime}} exp\left(\sum_{j = 1}^m \sum_{i = 1}^n \lambda_j f_j(x, i, y^\prime_i, l^\prime_{i-1})\right)} $$

Linear-Chain CRF特征函数的定义非常灵活, 不同的形式用于不同的功能. 比如对于HMM而言, 不管输入怎么变, 状态转换$transition(i, j)$的分值是一样的$\log p (y_t = j | y_{t−1} = i)$; 那么此时在CRF中, 我们通过增加这样一个特征$1_{\{y_{t}=j\}} 1_{\{y_{t-1}=1\}} 1_{\{x_{t}=o\}}$, 使$transition(i, j)$分值依赖于当前的观察序列: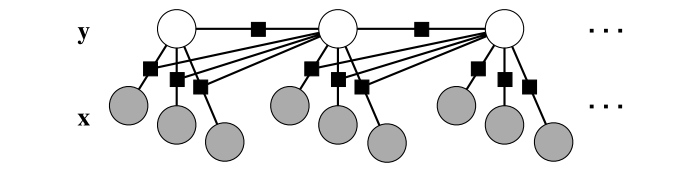

这种特征常常用于文本处理中, 比如:

  1. 一个句子提供观察值$x_{i-1, i}$
  2. 单词的标签$y_{i-1, i}$

需要指出的是在线性链CRF的定义中每个feature的依赖值并不仅限于当前和上一时间步的观察值. 事实上, 因为CRF并不表达变量之间的依赖关系, 我们可以让因子$\Psi_{t}$依赖于整个观察向量$x$并保持线性图结构, 这时候的特征函数就是$f_{k}\left(y_{t}, y_{t-1}, \mathbf{x}\right)$, 可以自由检视所有输入变量$x$, 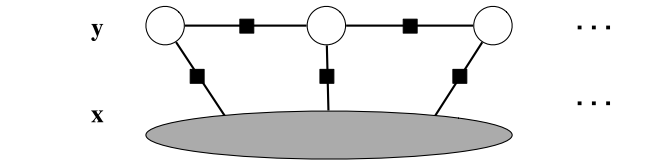这个特性可以拓展到所有CRFs而不仅限于线性链CRF.

CRF既具有判别式模型的优点，又考虑到长距离上下文标记间的转移概率，以序列化形式进行全局参数优化和解码的特点，解决了其他判别式模型(如MEMM)难以避免的标记偏见问题。

隐马尔可夫模型和Linear-Chain CRF的联系

HMM的生成式概率模型是$p(y,x)$, 它的条件概率$p(y|x)$本质上就是选取了特定特征函数的CRF. HMM和CRF的对应关系类似于Naive-Bayes和Logistics regression, 都是生成式和判别式的对比. HMM则采用生成式方法进行标签生成, CRF将各种特征组合在一起判断标签. HMM可以推演出特定形式的CRF. 把上式的HMM改写成如下形式:

$$ \begin{aligned} p(y, x)=& \frac{1}{Z} \prod_{t=1}^T \exp \left( \sum_{i, j \in S} \theta_{i j} 1_{\{y_t=i\}} 1_{\{y_{t-1}=j\}} \right. \\ &\left.+ \sum_{i \in S} \sum_{o \in O} \mu_{o i} 1_{\{y_{t}=i\}} 1_{\{x_{t}=o\}} \right) \end{aligned} $$

其中$\theta=\{\theta_{i j}, \mu_{o i}\}$是分布的实参数, $Z$是常数正则项. $$ \begin{aligned} \theta_{i j} &=\log p\left(y^{\prime}=i | y=j\right) \\ \mu_{o i} &=\log p(x=o | y=i) \\ Z &=1 \end{aligned} $$

HMM是生成式的, 借鉴Naive Bayes 到 logistics regression的方式, 通过引入特征函数这个概念, $f_{k}\left(y_{t}, y_{t-1}, x_{t}\right)$, 对于每一个$(i, j)$跳转, 加入特征函数$f_{i j}\left(y, y^{\prime}, x\right)=1_{\{y=i\}} 1_{\{y^{\prime}=j\}}$, 对于每一个状态-观察值对$(i,o)$, 加入特征函数$f_{i o}\left(y, y^{\prime}, x\right)=1_{\{y=i\}} \mathbf{1}_{\{x=o\}}$. 以上特征函数统一表示为$f_k$, 那么可以进一步把HMM写成:

$$p(\mathbf{y}, \mathbf{x})=\frac{1}{Z} \prod_{t=1}^{T} \exp \left(\sum_{k=1}^{K} \theta_{k} f_{k}\left(y_{t}, y_{t-1}, x_{t}\right)\right)$$

可以得出条件概率$p(y|x)$

$$p(\mathbf{y} | \mathbf{x})=\frac{p(\mathbf{y}, \mathbf{x})}{\sum_{\mathbf{y}^{\prime}} p\left(\mathbf{y}^{\prime}, \mathbf{x}\right)}=\frac{\prod_{t=1}^{T} \exp \left(\sum_{k=1}^{K} \theta_{k} f_{k}\left(y_{t}, y_{t-1}, x_{t}\right)\right)}{\sum_{\mathbf{y}^{\prime}} \prod_{t=1}^{T} \exp \left(\sum_{k=1}^{K} \theta_{k} f_{k}\left(y_{t}^{\prime}, y_{t-1}^{\prime}, x_{t}\right)\right)}$$

所以当联合概率$p(y,x)$以HMM的形式因式分解, 则关联的条件分布$p(y|x)$就是一种特定形式的linear-chain CRF，即一种仅使用当前单词自身作为特征的CRF.

通过恰当地设置特征函数, 可以从CRF中构建出一个HMM. 在CRF的对数线性形式中, 设置权重为对应HMM(取对数后)的二元转换和发射概率: $\log p(s,o) = \log p(s_0) + \sum_i \log p(s_i | s_{i-1}) + \sum_i \log p(o_i | s_i)$

  • 对于每个状态pair$\left(y_{i-1}, y_i\right)$, 对应HMM的每个状态转换概率$p(s_i = y_i | s_{i-1} = y_{i-1})$, CRF定义一组特征函数为$f_{y_{i-1},y_i}(o, i, s_i, s_{i-1}) = 1$ 如果 $s_i = y_i$ 且 $s_{i-1} = y_{i-1}$, 为这些特征赋予权重$g_{y_{i-1},y_i} = \log p(s_i = y_i | s_{i-1} = y_{i-1})$
  • 对于每个状态-观察值pair, 对应HMM的每个发射概率$p(o_i = x | s_{i} = y_i)$, CRF定义一组特征函数为$f_{x,y}(o, i, s_i, s_{i-1}) = 1$ 如果 $o_i = x$ 且 $s_i = y_i$, 赋予权重$w_{x,y} = \log p(o_i = x | s_i = y)$.

如此, CRF计算的似然$p(y|x)$就精确地正比于对应的HMM, 也就是说, 任意的HMM都可以由CRF表达出来.

CRF比HMM更强大, 更泛用

  1. CRF可以定义更广泛的特征函数：HMM受限于相邻位置的状态转换（二元转换）和发射概率函数，迫使每个单词仅依赖于当前标签，并且每个标签仅依赖于前一个标签。而CRF可以使用更多样的全局特征。例如，如果句子的结尾包含问号，则可以给给CRF模型增加一个特征函数，记录此时将句子的第一个单词标记为VERB的概率。这使得CRF可以使用长距离依赖的特征。
  2. CRF可以有任意的权重值：HMM的概率值必须满足特定的约束， $0 <= p(o_i | s_i) <= 1, \sum_o p(o_i = x | y_1) = 1)$, 而CRF的权重值是不受限制的。

CRF与Logistic Regression

CRF的概率计算与Logistic Regression (LR)的形式类似， $$CRF: p(l | s) = \frac{exp \left(\sum_{j = 1}^m \sum_{i = 1}^n \lambda_j f_j(s, i, l_i, l_{i-1})\right)}{\sum_{l’} exp\left(\sum_{j = 1}^m \sum_{i = 1}^n \lambda_j f_j(s, i, l^\prime_i, l^\prime_{i-1})\right)}$$

$$LR: P(y|x) = \frac{\exp \bigg( \sum\limits_{i=1}^{N} w_{i} \cdot f_{i}(x,y) \bigg)} {\sum\limits_{y’ \in Y} \exp \bigg( \sum\limits_{i=1}^{N} w_{i} \cdot f_{i}(x,y’) \bigg)}$$ 在LR中, $f_i(y, x)$是一个特征，$w_i$是与该特征相关的权重。提取的特征是二元特征，取值0或1，通常称为指示函数。这些特征中的每一个都由与输入$x$和分类$y$相关联的函数计算。

实际上，CRF基本上就是逻辑回归的序列化：与逻辑回归是用于分类的对数线性模型不同，CRF是标签序列的对数线性模型。

CRF模型训练

如何通过数据训练CRF模型, 估计特征函数的权重? 利用极大似然估计（Maximum Likelihood Estimation，MLE)和梯度优化(gradient descent).

$\log p(l | s)$相对于参数$λ_i$的梯度为:

$$\frac{\partial}{\partial w_j} \log p(l | s) = \sum_{j = 1}^m f_i(s, j, l_j, l_{j-1}) - \sum_{l’} p(l’ | s) \sum_{j = 1}^m f_i(s, j, l^\prime_j, l^\prime_{j-1})$$

导数的第一项是真实标签下的特征$f_i$的贡献，第二项是当前模型下特征$f_i$的期望贡献。

对于一堆训练样例（句子和相关的词性标签）。随机初始化CRF模型的权重。要将这些随机初始化的权重转移到正确的权重，对于每个训练示例:

  • 遍历每个特征函数$f_i$，计算训练示例相对于$λ_i$的对数概率的梯度
  • 以learning rate $\alpha$的速率沿梯度方向不断修正$λ_i$:

$$\lambda_i = \lambda_i + \alpha [\sum_{j = 1}^m f_i(s, j, l_j, l_{j-1}) - \sum_{l’} p(l’ | s) \sum_{j = 1}^m f_i(s, j, l^\prime_j, l^\prime_{j-1})]$$

  • 重复这些训练步骤，直到满足停止条件（例如，更新低于某个阈值）。

CRF的缺点是模型训练时收敛速度比较慢.

训练后的CRF模型, 可以用于预测一个未标记序列的最大可能标记. 我们需要每个标记的概率$p(l | s)$, 对于大小为k的标签集和长度为m的句子, 需要比较的$p(l | s)$组合有$k^m$种. 但是计算时, 可以利用动态规划的方法, 原理类似于Viterbi算法.

Tensorflow实现的CRF就是线性链CRF $$\begin{aligned}&P_Q(a_1,a_2,\dots,a_n)\ =&\frac{1}{Z} \exp \Big[f(a_1;Q)+g(a_1, a_2;Q) + f(a_2;Q) +\dots + g(a_{n-1}, a_n;Q) + f(a_n;Q)\Big] \end{aligned}$$ 所谓线性链，就是直接认为函数$g$实际上跟$Q$没关系，即对于任何的输入文本，$g(a_{k-1},a_k)$是个常数矩阵。剩下的则跟逐标签softmax的情形差不多了，认为$f(a_k;Q)\equiv f(a_k;q_k)$. 相对于逐标签softmax，CRF只是换了一个loss，多了一个转移矩阵，并且解码的时候需要用到viterbi算法。按照极大似然的思想，loss应该取为： $$\begin{aligned} &-\log P_Q(a_1,a_2,\dots,a_n)\ =& - \sum_{k=1}^n f(a_k;q_k) - \sum_{k=2}^n g(a_{k-1},a_k) + \log Z \end{aligned}$$

如果前面模型用BERT或者BiLSTM来得到特征$q_k$，那么就得到了序列标注任务中的Encoder-CRF了。

CRF中文命名实体识别

比如中文命名实体识别任务, 假如需要判断人名、地名、组织名三类命名实体.

对于人名, 通过一些模板来筛选特征。模板是对上下文的特定位置和特定信息的考虑, 适用于人名的特征模板:

  • 人名的指界词：主要包括称谓词、动词和副词等，句首位置和标点符号也可。根据指界词与人名共现的概率的大小，将人名的左右指界词各分为两级，生成4个人名指界词列表：
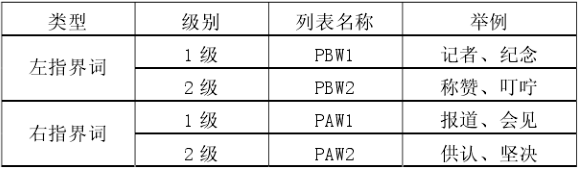
  • 人名识别特征的原子模板，每个模板都只考虑了一种因素：

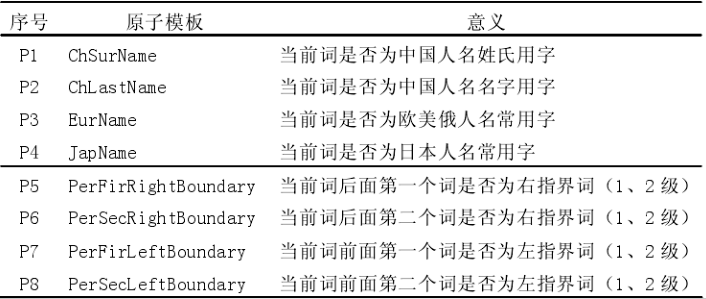
当特征函数取特定值时，特征模板被实例化, 就可以得到具体的特征。比如当前词的前一个词 $w_{i-1}$ 在人名1级左指界词列表中出现, $f_i(x, y) = 1, if: PBW1(w_{i-1}) = true, y = PERSON$

类似的，做地名、组织名的特征提取和选择，并将其实例化，得到所有的特征函数。

评测指标: 召回 recall = $ \frac{正确识别的命名实体首部（尾部）的个数}{标准结果中命名实体首部（尾部）的的总数} \times 100%$

精确率 precision = $ \frac{正确识别的命名实体首部（尾部）的个数}{识别出的命名实体首部（尾部）的总数} \times 100%$

F1 = $ \frac{2 \times precision \times recall}{precision + recall}$

谈谈生成式模型和判别式模型

从朴素贝叶斯, 到HMM; 从Logistic Regression到CRF, 这些概率图模型有如下转换关系:

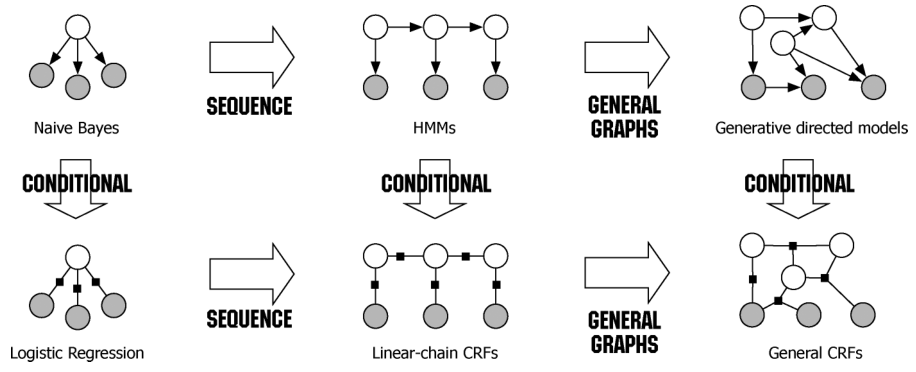
而在朴素贝叶斯与Logistic Regression, 以及HMM和CRF之间, 又有生成式和判别式的区别.

  • 生成式模型描述标签向量y如何有概率地生成特征向量x, 即尝试构建x和y的联合分布$p(y, x)$, 典型的模型有HMM，贝叶斯模型，MRF。生成式模型
  • 而判别模型直接描述如何根据特征向量x判断其标签y, 即尝试构建$p(y | x)$的条件概率分布, 典型模型如如LR, SVM，CRF，MEMM等. 不构建$p(x)$是因为分类时用不到.

原则上，任何类型的模型都可以使用贝叶斯规则转换为另一种类型，但实际上这些方法是不同的. 生成模型和判别模型都描述了$p(y, x)$的概率分布，但努力的方向不同。生成模型，例如朴素贝叶斯分类器和HMM，是一类可以因式分解为$p(y, x) = p(y)p(x|y)$的联合分布, 也就是说，它们描述了如何为给定标签的特征采样或“生成”值。生成式模型从统计的角度表示数据的分布情况，能够反映同类数据本身的相似度，不关心判别边界。生成式模型的优点是: • 实际上带的信息要比判别模型丰富， 研究单类问题比判别模型灵活性强 • 能更充分的利用先验知识 • 模型可以通过增量学习得到 缺点也很明显: • 学习过程比较复杂; • 在目标分类问题中准确度不高

而判别式模型, 比如 LR, 是一系列条件分布$p(y | x)$. 也就是说，分类规则是直接建模的。原则上，判别模型也可通过为输入提供边际分布$p(x)$来获得联合分布$p(y, x)$，但很少需要这样。条件分布$p(y | x)$不包括$p(x)$的信息，在分类任务中其实无论如何也用不到。其次，对$p(x)$建模的困难之处在于它通常包含很多建模难度较高的有高度依赖性的特征。判别式模型寻找不同类别之间的最优分类面，反映的是异类数据之间的差异。优点是: • 分类边界更灵活，比使用纯概率方法或生产模型得到的更高级。 • 能清晰的分辨出多类或某一类与其他类之间的差异特征 • 在聚类、viewpoint changes, partial occlusion and scale variations中的效果较好 •适用于较多类别的识别 缺点是：• 不能反映训练数据本身的特性。• 能力有限，可以分类, 但无法把整个场景描述出来。

参考资料

  1. An Introduction to Conditional Random Fields, Sutton, C., & McCallum, A. (2011)
  2. http://blog.echen.me/2012/01/03/introduction-to-conditional-random-fields/
  3. Classical probabilistic models and conditional random fields
  4. https://kexue.fm/archives/5542
  5. McCallum, A. (1909). Maximum Entropy Markov Models for Information Extraction and Segmentation. Berichte Der Deutschen Chemischen Gesellschaft, 42(1), 310–317. https://doi.org/10.1002/cber.19090420146