Resource and Reference:
- CS61B Berkeley - Josh Hug
- Algorithms Princeton - ROBERT SEDGEWICK, KEVIN WAYNE
效率来源两个方面:
- 编程成本: 开发程序需要多长时间?代码是否容易阅读,修改和维护(大部分成本来自维护和可扩展性)?
- 运行成本: 程序需要多长时间运行 (Time complexity)? 需要多少内存 (Space complexity)?
Asymptotic Analysis
Care about what happens for very large N (asymptotic behavior). We want to consider what types of algorithms would best handle scalability - Algorithms that scale well have better asymptotic runtime behavior.
Simplification Summary
- Only consider the worst case.
- Pick a representative operation (aka: cost model)
- Ignore lower order terms
- Ignore multiplicative constants.
Simplified Analysis Process
- Choose cost model (representative operation)
- Figure out the order of growth for the count of representative operation by either:
- Making an exact count, and discarding unnecessary pieces
- Only consider the worst case.
- Ignore lower order terms
- Ignore constants.
- Or, using intuition/inspection to determine orders of growth.
- Making an exact count, and discarding unnecessary pieces
Big Theta
Formalizing Order of Growth: Suppose a function $R(N)$ with order of growth $f(N)$, this is represented as $R(N) \in \Theta(f(N))$ in notation. Means that there exists positive constants $k_1, k_2$ such that:
$$k_1 ⋅ f(N) ≤ R(N) ≤ k_2 ⋅ f(N),$$for all values of $N$ greater than some $N_0$(a very large N).
Procedure:
- Given a piece of code, express its runtime as a function $R(N)$
- $N$ is some property of the input of the function. Oftentimes, $N$ represents the size of the input
- Rather than finding $R(N)$ exactly, instead care about the order of growth of $R(N)$.
- One approach (not universal):
- Choose a representative operation
- Let $C(N)$ = count of how many times that operation occurs, as a function of $N$.
- Determine order of growth $C(N) \in \Theta(f(N))$
- Often (but not always) consider the worst case count.
- If operation takes constant time, then $R(N) \in \Theta(f(N))$
在 Big Theta 的范畴内,对于涉及 logarithm 的情况,底数并不重要,任何底数都是等价的: Binary search: $\Theta(\log N)$ 直接忽略底数符号。 Selection sort: $\Theta(N^2)$ Merge two sorted array (Merge Sort): $\Theta(N)$
用 merge sort 加速 selection sort - 把 selection sort 递归地平分, 总共能分解出$\log_2N$个 merge sorts, 伪代码:
If the list is size 1:
return
else:
Mergesort the left half
Mergesort the right half
Merge the results
Total runtime is $≈Nk$, where $k = \log_2(N)$ is the number of levels, overall runtime is $\Theta(N \log N)$. $N^2$ vs. $N \log N$ is an enormous difference. Going from $N\log N$ to $N$ is nice, but not a radical change.
Useful math: $1 + 2 + 3 + ... + N = N * (N + 1) / 2 = \Theta(N^2)$ $1 + 2 + 4 + ... + N = 2N - 1 = \Theta(N)$
To estimate a discrete sum, replace the sum with an integral, and use calculus: $1 + 2 + 3 + ... + N = \sum_{i=1}^{N} i \sim \int_{x=1}^N x dx \sim \frac{1}{2}(N^2)$
$1^k + 2^k + ... + N^k = \sum_{i=1}^{N} i^k \sim \int_{x=1}^N x^k dx \sim \frac{1}{k+1}(N^{k+1})$
$1 + 1/2 + 1/3 + … + 1/N = \sum_{i=1}^{N} i^{-1} \sim \int_{x=1}^N x^{-1} dx \sim \ln N$
3-sum triple loop, $\sum_{i=1}^{N}\sum_{j=1}^{N}\sum_{k=1}^{N} 1 \sim \int_{x=1}^N\int_{y=x}^N\int_{z=y}^N dz dy dx \sim \frac{1}{6}N^3$
Big O
Big Theta expresses the exact order of as a function of the input size. However, if the runtime depends on more than just the size of the input, then we must qualify our statements into different cases before using Big Theta.
Big O: $R(N) \in O(f(N))$, means that there exists positive constants $k_2$, such that: $R(N) \leq k_2 \cdot f(N)$ for all values of $N$ greater than some $N_0$(a very large $N$). This is a looser condition than Big Theta since Big O does not care about the lower bound, thus it is less informative than Big Theta.
To summarize the usefulness of Big O:
- It allows us to make simple statements without case qualifications, in cases where the runtime is different for different inputs.
- Sometimes, for particularly tricky problems, we (the computer science community) don’t know the exact runtime, so we may only state an upper bound.
- It’s a lot easier to write proofs for Big O than Big Theta, like we saw in finding the runtime of mergesort in the previous chapter. This is beyond the scope of this course.
类似的也可以定义一个下限概念 - Big Omega ($\Omega$), 一般用于表明一个问题的难度有多大。
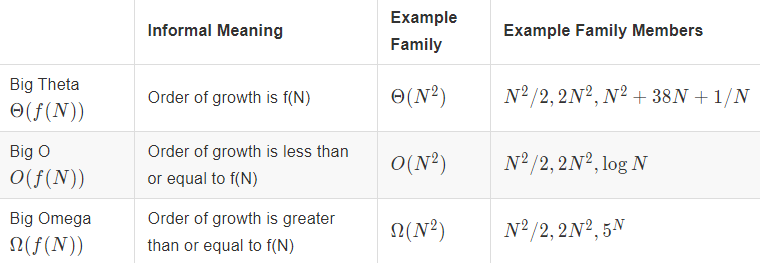
Summary
- Big O is an upper bound (“less than or equals”)
- Big Omega is a lower bound (“greater than or equals”)
- Big Theta is both an upper and lower bound (“equals”)
- Big O does NOT mean “worst case”. We can still describe worst cases using Big Theta
- Big Omega does NOT mean “best case”. We can still describe best cases using Big Theta
- Big O is sometimes colloquially used in cases where Big Theta would provide a more precise statement – from: https://joshhug.gitbooks.io/