Union−Find

Considering the dynamic connectivity problem, modeling of multiple objects connected in a space/network.

Applications involve manipulating objects of all types. ・Pixels in a digital photo. ・Computers in a network. ・Friends in a social network. ・Transistors in a computer chip.

Given a set of N objects.

  • union(a, b): connect two objects.
  • connected(p, q): is two objects connected?
  • find(p): Find component identifier for p (0 to N – 1)

Modeling the objects: array.

Modeling the connections: Maximal set of objects that are mutually connected - Connected components.

Data structure:

  1. Quick find Integer array id[] of length N, two objects are connected iff they have the same id. Defect: union too expensive, $\in \Theta(N^2)$.

  2. Quick-union Integer array id[] of length N, id[i] is parent of i, root of i is id[id[id[...id[i]...]]] (until it doesn’t chang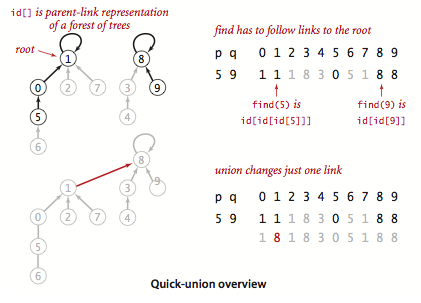e). The find is recursive.

    /** chase parent pointers until reach root
 * (depth of i array accesses) */
private int find(int i) {
    while (i != id[i]) i = id[i];
    return i;
}

    Defect: Trees can get tall, find too expensive, $\in \Theta(N)$.

  3. Weighted quick-union Modify quick-union to avoid tall trees. Balance by linking root of smaller tree to root of larger tree. Maintain extra array sz[i] to keep track of size of each tree (number of objects).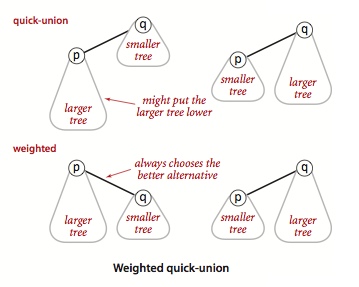 find: time proportional to depth of p and q, the depth of any node x is at most $\log N$,

  4. Weighted quick-union with path compression Making all the nodes that examined directly link to its root. Keeps tree almost completely flat.

/** Make every other node in path point to its grandparent
* (thereby halving path length). */
private int root(int i) {
    while (i != id[i]) {
        id[i] = id[id[i]];
        i = id[i];
    }
    return i;
}

Amortized analysis: `[Hopcroft-Ulman, Tarjan]` Starting from an empty data structure, any sequence of M union-find ops on N objects makes $≤ c ( N + M \lg \ast N )$ array accesses. $\lg \ast N$ is [Iterated logarithm](https://en.wikipedia.org/wiki/Iterated_logarithm), for $N = 2^{65536}$, $\lg \ast N = 5$. In theory, WQUPC is not quite linear. In practice, WQUPC is linear.

Amazing fact. [Fredman-Saks] No linear-time algorithm exists.

Element Sort

Two elementary sorting methods: selection sort and insertion sort. Shellsort is a variation of one of them.

The objective is to rearrange the items such that their keys are in ascending order.

In Java, the abstract notion of a key is captured by the Comparable interface. The Comparable interface provides an elegant API for callback when Java need to compare keys.

Some background knowlege:

  • Cost model, please refer to Asymptotic Analysis
  • Sorting cost model. How many compares and exchanges, or array accesses, for a sorting.
  • Memory. There are sorting algorithms that sort in place (no extra memory except perhaps for a small function-call stack or a constant number of instance variables), and those that need enough extra memory to hold another copy of the array to be sorted.

Selection Sort

Repeatedly selecting the smallest remaining item:

  1. Find the smallest item in the array, and exchange it with the first entry.
  2. Find the next smallest item and exchange it with the second entry.
  3. Continue until the entire array is sorted.

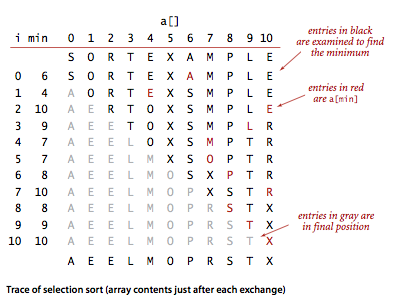
Selection sort uses ~$n^2/2$ compares and n exchanges to sort an array of length n.

Insertion Sort

Works like people sort Pokers: consider the cards one at a time, inserting each into its proper place among those already considered (keeping them sorted). 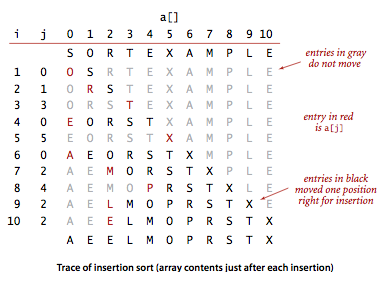In a computer implementation, we need to make space for the current item by moving larger items one position to the right, before inserting the current item into the vacated position.

For randomly ordered arrays of length N with distinct keys, insertion sort uses ~$N^2/4$ compares and ~$N^2/4$ exchanges on the average. The worst case is ~ $N^2/2$ compares and ~ $N^2/2$ exchanges and the best case is $N-1$ compares and 0 exchanges.

Insertion sort works well for certain types of nonrandom arrays that often arise in practice, even if they are huge. An inversion is a pair of keys that are out of order in the array. For instance, E X A M P L E has 11 inversions: E-A, X-A, X-M, X-P, X-L, X-E, M-L, M-E, P-L, P-E, and L-E. If the number of inversions in an array is less than a constant multiple of the array size, we say that the array is partially sorted.

Shellsort

Shellsort gains speed by allowing exchanges of entries that are far apart, to produce partially sorted arrays that can be efficiently sorted, eventually by insertion sort.

The idea is to rearrange the array to give it the property that taking every $h_{th}$ entry (starting anywhere) yields a sorted sequence. Such an array is said to be h-sorted. By h-sorting for some large values of h, we can move entries in the array long distances and thus make it easier to h-sort for smaller values of h. Using such a procedure for any increment sequence of values of h that ends in 1 will produce a sorted array:

The number of compares used by shellsort with the increments 1, 4, 13, 40, 121, 364, … is O(N^{3/2}).

Merge Sort

Merging means combining two ordered arrays to make one larger ordered array. Merge sort is an utility of divide and conquer paradigm.

Mergesort guarantees to sort an array of N items in time proportional to $N \log N$, no matter what the input. But it uses extra space proportional to N. Specifically, mergesort uses between $1/2 N \lg N$ and $N \lg N$ compares and at most $6 N \lg N$ array accesses to sort any array of length N.

Abstract in-place merge: The method merge(a, lo, mid, hi) in Merge.java puts the results of merging the subarrays a[lo..mid] with a[mid+1..hi] into a single ordered array, leaving the result in a[lo..hi]. While it would be desirable to implement this method without using a significant amount of extra space, such solutions are remarkably complicated.

public class Merge
{
    private static void merge(Comparable[] a, Comparable[] aux, int lo, int mid, int hi)
    {
       assert isSorted(a, lo, mid);   // precondition: a[lo..mid]   sorted
       assert isSorted(a, mid+1, hi); // precondition: a[mid+1..hi] sorted

       for (int k = lo; k <= hi; k++) // copy
          aux[k] = a[k];

       int i = lo, j = mid+1;
       for (int k = lo; k <= hi; k++) // merge
       {
          if      (i > mid)              a[k] = aux[j++];
          else if (j > hi)               a[k] = aux[i++];
          else if (less(aux[j], aux[i])) a[k] = aux[j++];
          else                           a[k] = aux[i++];
       }

       assert isSorted(a, lo, hi);     // postcondition: a[lo..hi] sorted
    }

    private static void sort(Comparable[] a, Comparable[] aux, int lo, int hi)
    {
       if (hi <= lo) return;
       int mid = lo + (hi - lo) / 2;
       sort(a, aux, lo, mid);
       sort(a, aux, mid+1, hi);
       merge(a, aux, lo, mid, hi);
    }

    public static void sort(Comparable[] a)
    {
       aux = new Comparable[a.length];
       sort(a, aux, 0, a.length - 1);
    }

}
}

Proposition. Mergesort uses at most $N lg N$ compares and $6 N lg N$ array accesses to sort any array of size N. Mergesort uses extra space proportional to N

A sorting algorithm is in-place if it uses $≤ c \log N$ extra memory. Ex. Insertion sort, selection sort, shellsort.

Mergesort: Practical improvements

Use insertion sort for small subarrays (7).

private static void sort(Comparable[] a, Comparable[] aux, int lo, int hi)
{
   if (hi <= lo + CUTOFF - 1)
   {
      Insertion.sort(a, lo, hi);
      return;
   }
   int mid = lo + (hi - lo) / 2;
   sort (a, aux, lo, mid);
   sort (a, aux, mid+1, hi);
   merge(a, aux, lo, mid, hi);
}

Stop if already sorted: Is biggest item in first half ≤ smallest item in second half?

private static void sort(Comparable[] a, Comparable[] aux, int lo, int hi)
{
   if (hi <= lo) return;
   int mid = lo + (hi - lo) / 2;
   sort (a, aux, lo, mid);
   sort (a, aux, mid+1, hi);
   if (!less(a[mid+1], a[mid])) return;
   merge(a, aux, lo, mid, hi);
}

Eliminate the copy to the auxiliary array. Save time (but not space) by switching the role of the input and auxiliary array in each recursive call.

private static void merge(Comparable[] a, Comparable[] aux, int lo, int mid, int hi)
{
   int i = lo, j = mid+1;
   for (int k = lo; k <= hi; k++) // merge from a[] to aux[]
   {
      if      (i > mid)          aux[k] = a[j++];
      else if (j > hi)           aux[k] = a[i++];
      else if (less(a[j], a[i])) aux[k] = a[j++];
      else                       aux[k] = a[i++];
   }
}

private static void sort(Comparable[] a, Comparable[] aux, int lo, int hi)
{
   if (hi <= lo) return;
   int mid = lo + (hi - lo) / 2;
   // switch roles of aux[] and a[]
   sort (aux, a, lo, mid);
   sort (aux, a, mid+1, hi);
   merge(a, aux, lo, mid, hi);
}

Top-down mergesort

A recursive mergesort implementation based on this abstract in-place merge.

Bottom-up mergesort

Do all the merges of tiny arrays on one pass, then do a second pass to merge those arrays in pairs, and so forth, continuing until we do a merge that encompasses the whole array.

  1. We start by doing a pass of 1-by-1 merges
  2. then a pass of 2-by-2 merges (merge subarrays of size 2 to make subarrays of size 4),
  3. then 4-by-4 merges, and so forth.

Proposition: No compare-based sorting algorithm can guarantee to sort N items with fewer than $lg(N!)$ ~ $N \lg N$ compares. Proposition. Mergesort is an asymptotically optimal compare-based sorting algorithm. That is, both the number of compares used by mergesort in the worst case and the minimum number of compares that any compare-based sorting algorithm can guarantee are ~N lg N.

public class MergeBU
{
   private static void merge(...)
   { /* as before */  }

   public static void sort(Comparable[] a)
   {
      int N = a.length;
      Comparable[] aux = new Comparable[N];
      for (int sz = 1; sz < N; sz = sz+sz)
         for (int lo = 0; lo < N-sz; lo += sz+sz)
            merge(a, aux, lo, lo+sz-1, Math.min(lo+sz+sz-1, N-1));
   }
}

About 10% slower than recursive, top-down mergesort on typical systems

Mergesort Applications

Java sort for objects. Perl, C++ stable sort, Python stable sort, Firefox JavaScript, …

Counting inversions: An inversion in an array a[] is a pair of entries a[i] and a[j] such that i < j but a[i] > a[j]. Given an array, design a linearithmic algorithm to count the number of inversion.

在数组中的两个数字，如果前面一个数字大于后面的数字，则这两个数字组成一个逆序对。输入一个数组,求出这个数组中的逆序对的总数P。并将P对1000000007取模的结果输出。 即输出P%1000000007

public int InversePairs(int [] array) {
    int len = array.length;
    int[] aux = new int[len];
    for (int k = 0; k < len; k++) // copy
        aux[k] = array[k];
    return InversePairsSort(array, aux, 0, len - 1);
}

private int InversePairsSort(int[] a, int[] b, int s, int e)
{
    if (e <= s) return 0;
    int mid = (e + s) / 2;
    int n1 = InversePairsSort(b, a, s, mid) % 1000000007;
    int n2 = InversePairsSort(b, a, mid + 1, e) % 1000000007;
    return (n1 + n2 + InversePairsMerge(a, b, s, mid, e)) % 1000000007;
}

private int InversePairsMerge(int[] a, int[] b, int s, int mid, int e)
{
    int i = mid, j = e, n = 0;
    for (int k = e; k >= s; k--)
    {// merge from a to b
        if (i < s)           b[k] = a[j--];
        else if (j <= mid)   b[k] = a[i--];
        else if (a[i] > a[j])
        {
                             n += j - mid;
                             if(n >= 1000000007)//数值过大求余
                                 n %= 1000000007;
                             b[k] = a[i--];
        }
        else                 b[k] = a[j--];
    }
    return n;
}

count while mergesorting.

Shuffling a linked list: Given a singly-linked list containing n items, rearrange the items uniformly at random. Your algorithm should consume a logarithmic (or constant) amount of extra memory and run in time proportional to $n \log n$ in the worst case:

Design a linear-time subroutine that can take two uniformly shuffled linked lists of sizes $n_1$ and $n_2$ and combined them into a uniformly shuffled linked lists of size $n_1 + n_2$.

Quick Sort

Basic plan:

  • Shuffle the array: Random shuffle. Probabilistic guarantee against worst case.
  • Partition so that, for some j
    • entry a[j] is in place
    • no larger entry to the left of j
    • no smaller entry to the right of j
  • Sort each piece recursively

Patition:

  • Repeat until i and j pointers cross.
    • Scan i from left to right so long as (a[i] < a[lo])
    • Scan j from right to left so long as (a[j] > a[lo])
    • Exchange a[i] with a[j]
  • When pointers cross. Exchange a[lo] with a[j]
public class Quick
{
    // return index of item now known to be in place
    private static int partition(Comparable[] a, int lo, int hi)
    {
       int i = lo, j = hi+1;
       while (true)
       {
          while (less(a[++i], a[lo])) // find item on left to swap
             if (i == hi) break;
          while (less(a[lo], a[--j])) // find item on right to swap
             if (j == lo) break;
          if (i >= j) break;          // check if pointers cross
          exch(a, i, j);
       }
       exch(a, lo, j);                // swap with partitioning item
       return j;
    }

    private static void sort(Comparable[] a, int lo, int hi)
    {
       if (hi <= lo) return;
       int j = partition(a, lo, hi);
       sort(a, lo, j-1);
       sort(a, j+1, hi);
    }

    public static void sort(Comparable[] a)
    {
       StdRandom.shuffle(a);
       sort(a, 0, a.length - 1);
    }
}

Best case. Number of compares is ~ $N \lg N$ Worst case. Number of compares is ~ $½N^2$ Average case. Number of compares is ~ $1.39 N \lg N$, 39% more compares than mergesort. But faster than mergesort in practice because of less data movement.

Quicksort: practical improvements

Insertion sort small subarrays (10 items), could delay insertion sort until one pass at end.

private static void sort(Comparable[] a, int lo, int hi)
{
   if (hi <= lo + CUTOFF - 1)
   {
      Insertion.sort(a, lo, hi);
      return;
   }

   int j = partition(a, lo, hi);
   sort(a, lo, j-1);
   sort(a, j+1, hi);
}

Median of sample: Best choice of pivot item = median. Estimate true median by taking median of sample. Median-of-3 (random) items

private static void sort(Comparable[] a, int lo, int hi)
{
   if (hi <= lo) return;

   int m = medianOf3(a, lo, lo + (hi - lo)/2, hi);
   swap(a, lo, m);

   int j = partition(a, lo, hi);
   sort(a, lo, j-1);
   sort(a, j+1, hi);
}

Quicksort with duplicate keys

・Algorithm goes quadratic unless partitioning stops on equal keys! ・1990s C user found this defect in qsort() Mistake. Put all items equal to the partitioning item on one side. Consequence. ~ $½N^2$ compares when all keys equal. Recommended. Stop scans on items equal to the partitioning item. Consequence. ~ $N \lg N$ compares when all keys equal.

3-way partitioning: Dutch national flag problem. Partition array into 3 parts so that: ・Entries between lt and gt equal to partition item v. ・No larger entries to left of lt. ・No smaller entries to right of gt.

  • Let v be partitioning item a[lo]
  • Scan i from left to right.
    • (a[i] < v): exchange a[lt] with a[i]; increment both lt and i
    • (a[i] > v): exchange a[gt] with a[i]; decrement gt
    • (a[i] == v): increment i
private static void sort(Comparable[] a, int lo, int hi)
{
   if (hi <= lo) return;
   int lt = lo, gt = hi;
   Comparable v = a[lo];
   int i = lo;
   while (i <= gt)
   {
      int cmp = a[i].compareTo(v);
      if      (cmp < 0) exch(a, lt++, i++);
      else if (cmp > 0) exch(a, i, gt--);
      else              i++;
   }
   sort(a, lo, lt - 1);
   sort(a, gt + 1, hi);
}

Quicksort Applications

Java sort for primitive types. C qsort, Unix, Visual C++, Python, Matlab, Chrome JavaScript, …

Selection: Order statistics, Find the “top k.” Given an array of N items, find a $k^{th}$ smallest item. Ex. Min(k = 0), max(k = N - 1), median(k = N/2).

Quick-select

  • Partition array so that:
    • Entry a[j] is in place
    • No larger entry to the left of j
    • No smaller entry to the right of j
  • Repeat in one subarray, depending on j; finished when j equals k.
public static Comparable select(Comparable[] a, int k)
{
    StdRandom.shuffle(a);
    int lo = 0, hi = a.length - 1;
    while (hi > lo)
    {
        int j = partition(a, lo, hi);
        if      (j < k) lo = j + 1;
        else if (j > k) hi = j - 1;
        else            return a[k];
    }
    return a[k];
}

Quick-select takes linear time on average.

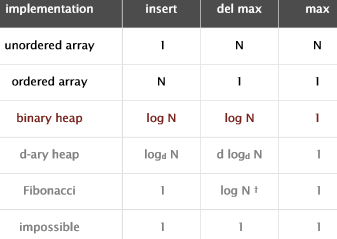
Priority Queues

优先队列可用于快速地（O(1)）返回最大或者最小的值。

public class MaxPQ<Key extends Comparable<Key>>
{
    MaxPQ() create an empty priority queue
    MaxPQ(Key[] a) create a priority queue with given keys
    void insert(Key v) insert a key into the priority queue
    Key delMax() return and remove the largest key
    boolean isEmpty() is the priority queue empty?
    Key max() return the largest key
    int size() number of entries in the priority queue
}

应用: ・Event-driven simulation. [customers in a line, colliding particles] ・Numerical computation. [reducing roundoff error] ・Data compression. [Huffman codes] ・Graph searching. [Dijkstra’s algorithm, Prim’s algorithm] ・Number theory. [sum of powers] ・Artificial intelligence. [A* search] ・Statistics. [maintain largest M values in a sequence] ・Operating systems. [load balancing, interrupt handling] ・Discrete optimization. [bin packing, scheduling] ・Spam filtering. [Bayesian spam filter]

比如对于数据流, 需要用优先队列保存最大的M个值, 因为内存不足以储存数据流全部数据.

Binary Heap

Heap-ordered binary tree: 父节点比其所有子节点都大（或都小）。根节点为最大值的binary heap称之为最大堆, 根节点为最小值的称之为最小堆.

以最大堆为例, 使用数组来表达：

  • 索引从1开始, 按照层次遍历顺序存储节点.
  • 最大值就是根节点a[1]\
  • 可以使用数组索引遍历树
    • 节点a[k]的父节点是a[k/2]
    • 节点a[k]的子节点为a[2k], a[2k+1]

当子节点的值比父节点大时, 需要不断调换二者的值, 直到不再有子节点比父节点大的情况存在:

private void swim(int k)
{
   while (k > 1 && less(k/2, k))
   {
      exch(k, k/2);
      k = k/2;
   }
}

反之当父节点比子节点小时:不断把父节点和较大的子节点调换, 直到恢复 heap order:

private void sink(int k)
{
   while (2*k <= N)
   {
      int j = 2*k;
      if (j < N && less(j, j+1)) j++;
      if (!less(k, j)) break;
      exch(k, j);
      k = j;
   }
}

插入操作, 需要先把新节点放在末端, 然后swim. 至多1 + lgN比较:

public void insert(Key x)
{
   pq[++N] = x;
   swim(N);
}

删除操作, 需要把根节点和尾节点调换, 然后sink, 至多2lgN比较

public Key delMax()
{
   Key max = pq[1];
   exch(1, N--);
   sink(1);
   pq[N+1] = null;
   return max;
}

public class MaxPQ<Key extends Comparable<Key>>
{
    private Key[] pq;
    private int N;
    public MaxPQ(int capacity)
    {  pq = (Key[]) new Comparable[capacity+1];  }
    public boolean isEmpty()
    {   return N == 0;   }
    public void insert(Key key)
    public Key delMax()
    {   /* see previous code */  }
    private void swim(int k)
    private void sink(int k)
    {   /* see previous code */  }
    private boolean less(int i, int j)
    {   return pq[i].compareTo(pq[j]) < 0;  }
    private void exch(int i, int j)
    {   Key t = pq[i]; pq[i] = pq[j]; pq[j] = t;  }
}

如果要实现最小堆, 那么就用greater()替代less()

Heap Sort

可以使用heap数据结构来排序一个数组，核心步骤是两个

  1. 创建一个最大堆
  2. 然后不断拿出当前最大值，放置于后面.
public class Heap
{
    public static void sort(Comparable[] a)
    {
        // bottom-up方法创建堆,
        // 虽然是 heap order, 但不一定是sorted order
        int N = a.length;
        for (int k = N/2; k >= 1; k--)
            sink(a, k, N);

        while (N > 1)
        { // 把当前最大值调换到N位置
         exch(a, 1, N); // 最大值放在尾部
         sink(a, 1, --N); // 恢复heap order
        }
   }

   private static void sink(Comparable[] a, int k, int N)
   {  /* as before */  }
   private static boolean less(Comparable[] a, int i, int j)
   {  /* as before */  }
   private static void exch(Comparable[] a, int i, int j)
   {  /* as before */  }
}

In-place sorting algorithm with N log N worst-case, but not stable

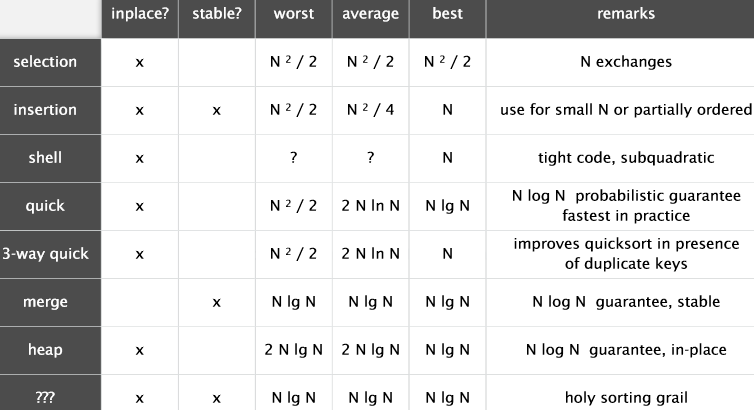
排序算法汇总比较

Pigeonhole sort

鸽巢排序(基数分类)

Pigeonhole sorting is a sorting algorithm that is suitable for sorting lists of elements where the number of elements (n) and the length of the range of possible key values (N) are approximately the same. It requires O(n + N) time.

  1. 给定要排序的数组，设置一个辅助数组作为初始的空“鸽笼”，通过原始数组的范围为每个键值设置一个鸽笼。
  2. 遍历原始数组，将每个值放入与其键对应的鸽笼中，这样每个鸽笼最终都包含该键的所有值的列表。
  3. 按顺序迭代鸽笼数组，并将非空鸽笼中的元素依次放回原始数组中。
/* Java program to implement Pigeonhole Sort */
public class GFG
{
    public static void pigeonhole_sort(int arr[], int n)
    {
        int min = arr[0];
        int max = arr[0];
        int range, i, j, index;

        for(int a=0; a<n; a++)
        {
            if(arr[a] > max)
                max = arr[a];
            if(arr[a] < min)
                min = arr[a];
        }

        range = max - min + 1;
        int[] phole = new int[range];
        //Arrays.fill(phole, 0);

        for(i = 0; i < n; i++)
            phole[arr[i] - min]++;

        index = 0;

        for(j = 0; j < range; j++)
            while(phole[j] > 0)
                arr[index++] = j + min;

    }

    public static void main(String[] args)
    {
        GFG sort = new GFG();
        int[] arr = {8, 3, 2, 7, 4, 6, 8};

        System.out.print("Sorted order is : ");

        sort.pigeonhole_sort(arr,arr.length);

        for(int i=0 ; i<arr.length ; i++)
            System.out.print(arr[i] + " ");
    }

}

类似于counting sort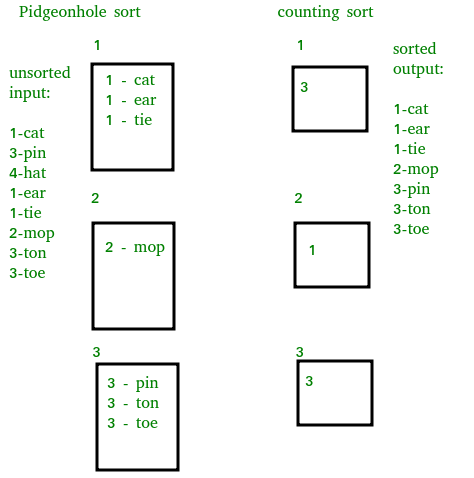

Bucket sort

桶排序(箱排序 bin sort)主要用于均匀分布区间值的排序，如浮点数排序，

distributing the elements of an array into a number of buckets. Each bucket is then sorted individually, either using a different sorting algorithm, or by recursively applying the bucket sorting algorithm. It is a distribution sort, a generalization of pigeonhole sort, and is a cousin of radix sort in the most-to-least significant digit flavor. Bucket sort can be implemented with comparisons and therefore can also be considered a comparison sort algorithm. The computational complexity estimates involve the number of buckets.

Worst-case performance ${\displaystyle O(n^{2})}$ Best-case performance ${\displaystyle \Omega (n+k)}$ Average performance ${\displaystyle \Theta (n+k)}$

  1. 设置一个初始为空的“桶”数组。
  2. Scatter：遍历原始数组，将每个对象分发到桶中。
  3. 对每个非空桶进行排序。
  4. Gather：按顺序访问桶并将所有元素放回原始数组中。

Graph

图：由边连接的成对的顶点集。

无向图，有向图