Adam Weight Decay in BERT

在看BERT(Devlin et al., 2019)的源码中优化器部分的实现时，发现有这么一段话

# Just adding the square of the weights to the loss function is *not*
# the correct way of using L2 regularization/weight decay with Adam,
# since that will interact with the m and v parameters in strange ways.
#
# Instead we want ot decay the weights in a manner that doesn't interact
# with the m/v parameters. This is equivalent to adding the square
# of the weights to the loss with plain (non-momentum) SGD.

其针对性地指出一些传统的Adam weight decay实现是错误的.

优化器回顾

先回顾一下几个优化器.

SGD和动量更新

SGD在所有参数上均采用全局且均等的学习率。

# Vanilla update
x += - learning_rate * dx

加入动量更新Momentum update一般都能得到更好的收敛速。动量更新可以从优化问题的物理角度出发来理解。损失函数可以解释为丘陵地形的高度（因此也可以解释为势能，U = mgh , 势能正比于高度）。

随机数初始化参数等效于在某个位置将初始速度设置为零。优化过程就等同于模拟参数矢量（即粒子）在损失函数的丘陵地形上滚动的过程。

由于作用在粒子上的力与势能的梯度有关（即$F = - \nabla U$），因此粒子所感受到的力正好是损失函数的（负）梯度。此外$F = ma$，因此（负）梯度在这个视角下和中与粒子的加速度成比例。因此梯度直接影响的是速度，由速度来影响位置.

# Momentum update
v = mu * v - learning_rate * dx # integrate velocity
x += v # integrate position

动量mu（一般取0.9）虽然叫动量，但其物理意义更像是摩擦系数. 它会衰减速度并降低系统的动能，避免粒子一直在山底震荡无法停止. 也就是在梯度方向有所改变的维度上的衰减速度. 同时可以在梯度方向不变的维度上维持速度，这样就可以加快收敛并减小震荡。

AdaGrad, RMSprop和Adam

我们希望优化器算法可以对每个参数自适应地调整学习率. AdaGrad(Duchi et al.)独立地适应模型的每个参数:

# Assume the gradient dx and parameter vector x
cache += dx**2
x += - learning_rate * dx / (np.sqrt(cache) + eps)

变量cache跟踪每个参数的梯度平方和。然后，将其用于element-wise地正则化参数更新。接收高梯度的权重将降低其有效学习率，而接收较小或不经常更新的权重将提高其有效学习率。 每个参数的学习率会缩放各参数反比于其历史梯度平方值总和的平方根.

RMSprop(Tieleman & Hinton, 2012)优化器也是一种自适应学习率方法, 不过没发表, 都是引用 slide 29 of Lecture 6 of Geoff Hinton’s Coursera class.

RMSProp对Adagrad进行如下调整:

cache = decay_rate * cache + (1 - decay_rate) * dx**2
x += - learning_rate * dx / (np.sqrt(cache) + eps)

使用了梯度平方的移动平均值, 避免激进的单调递减的学习率。 decay_rate一般取[0.9, 0.99, 0.999].

Adam (Kingma & Ba, 2014)可以看做动量法和RMSprop的结合, 结合了AdaGrad处理稀疏梯度的能力和RMSProp处理不平稳目标函数的能力。简化的实现:

m = beta1*m + (1-beta1)*dx
v = beta2*v + (1-beta2)*(dx**2)
x += - learning_rate * m / (np.sqrt(v) + eps)

看起来与RMSProp更新完全相同，只是使用了渐变m的“平滑”版本而不是原始（且可能是嘈杂的）梯度dx。文章建议值为eps = 1e-8, beta1 = 0.9, beta2 = 0.999

在MNIST数据上做的简单对比实验:

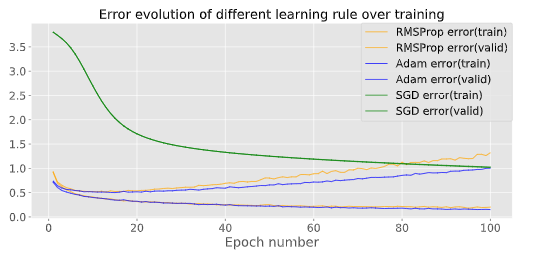
引用cs231的图:

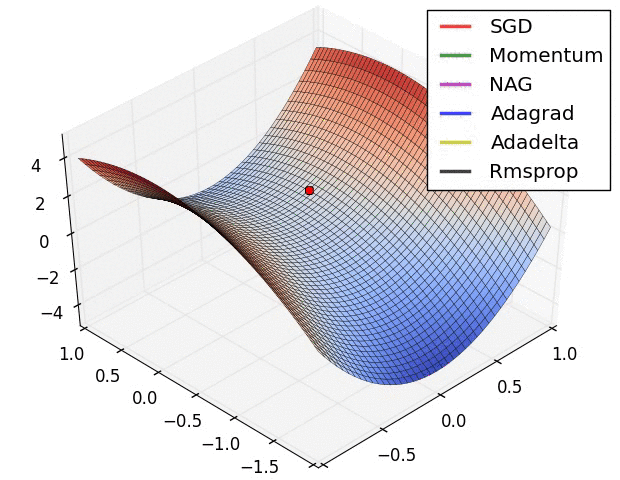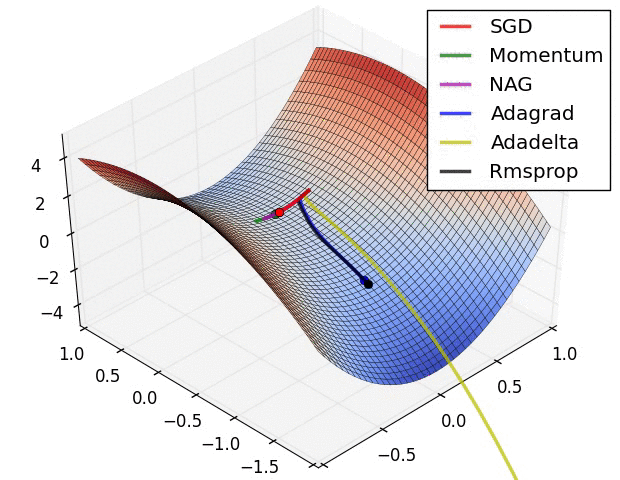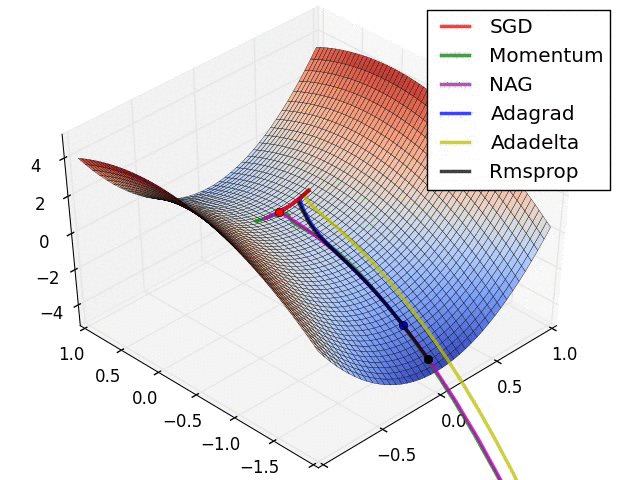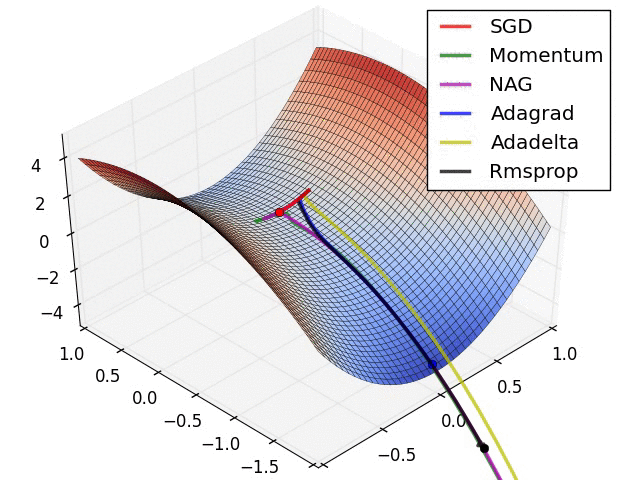
Adam Weight Decay 和 L2正则化

以前在训练语言模型时, 发现精调的SGD比Adam得到的最终效果更好. 可见Adam的优势并不如原来文章所言. 在2017年的论文《Fixing Weight Decay Regularization in Adam》(后来更新第三版为Decoupled Weight Decay Regularization, Loshchilov 2017)[#refer]中提出了Adam Weight Decay的方法用于修复Adam的权重衰减错误。问题在于目前大多数DL框架的L2 regularization实现用的是weight decay的方式，而weight decay在与Adam共同使用的时候有互相耦合。

L2 regularization: 给参数加上一个L2惩罚 $$ f_{t}^{r e g}(\mathbb{\theta})=f_{t}(\mathbb{\theta})+\frac{\lambda^{\prime}}{2}|\mathbb{\theta}|_{2}^{2} $$ 用程序表达是:

final_loss = loss + weight_decay_r * all_weights.pow(2).sum() / 2

Hanson & Pratt (1988)的Weight decay让weight $\theta$以$\lambda$的速率指数衰减: $$ \theta_{t+1}=(1-\lambda) \theta_{t}-\alpha \nabla f_{t}\left(\theta_{t}\right), $$ 在vanilla SGD中用程序表达是:

w = w - lr * w.grad - lr * weight_decay_r * w

大部分库都使用第一个实现。不过实际上几乎总是通过在梯度上添加 weight_decay_r * w来实现，而不是实际更改损失函数。）

在标准SGD的情况下，通过对衰减系数做变换，令$\lambda^{\prime}=\frac{\lambda}{\alpha}$, L2正则则等价于Weight Decay. 但是其他情况下, 比如增加了momentum后, L2正则化和权重衰减并不等价。

both mechanisms push weights closer to zero, at the same rate

fast ai的代码解释是, 在momentum SGD中使用L2正则就需要把weight_decay_r * w加到梯度中. 但是梯度不是直接在weights中减去, 而是要通过移动平均

moving_avg = alpha * moving_avg + (1-alpha) * (w.grad + weight_decay_r*w)

该移动平均值再乘以学习率，然后从weights中减去.

而权重衰减则是:

moving_avg = alpha * moving_avg + (1-alpha) * w.grad 
w = w - lr * moving_avg - lr * wd * w

很明显二者会不同的.

在自适应优化器Adam中情况类似, 主要体现在以下二者:

  1. the sums of the gradient of the loss function
  2. the gradient of the regularizer (i.e., the L2 norm of the weights)

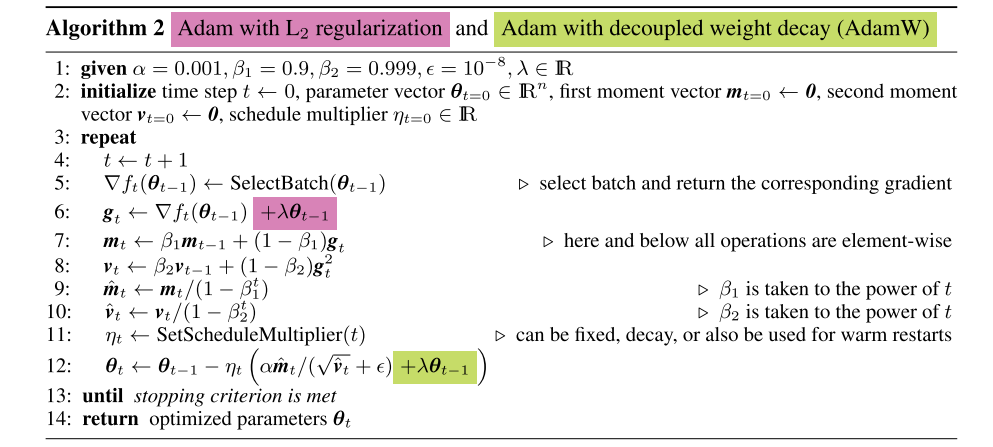
红色是Adam+L2 regularization的方式，梯度$g_t$的移动平均 $m_t$ 与梯度平方的移动平均 $v_t$ 都加入了$\lambda \theta_{t- 1}$

如何解释这种不同? 直接引用文章原文:

with decoupled weight decay, only the gradients of the loss function are adapted (with the weight decay step separated from the adaptive gradient mechanism)

With L2 regularization both types of gradients are normalized by their typical (summed) magnitudes, and therefore weights x with large typical gradient magnitude s are regularized by a smaller relative amount than other weights.

decoupled weight decay regularizes all weights with the same rate λ, effectively regularizing weights x with large s more than standard L2 regularization

BERT源码中的apply_gradients给出了修正方法:

def apply_gradients(self, grads_and_vars, global_step=None, name=None):
  """See base class."""
  assignments = []
  for (grad, param) in grads_and_vars:
    if grad is None or param is None:
      continue

    param_name = self._get_variable_name(param.name)

    m = tf.get_variable(
        name=param_name + "/adam_m",
        shape=param.shape.as_list(),
        dtype=tf.float32,
        trainable=False,
        initializer=tf.zeros_initializer())
    v = tf.get_variable(
        name=param_name + "/adam_v",
        shape=param.shape.as_list(),
        dtype=tf.float32,
        trainable=False,
        initializer=tf.zeros_initializer())

    # Standard Adam update.
    next_m = (
        tf.multiply(self.beta_1, m) + tf.multiply(1.0 - self.beta_1, grad))
    next_v = (
        tf.multiply(self.beta_2, v) + tf.multiply(1.0 - self.beta_2,
                                                  tf.square(grad)))

    update = next_m / (tf.sqrt(next_v) + self.epsilon)

    # Just adding the square of the weights to the loss function is *not*
    # the correct way of using L2 regularization/weight decay with Adam,
    # since that will interact with the m and v parameters in strange ways.
    #
    # Instead we want ot decay the weights in a manner that doesn't interact
    # with the m/v parameters. This is equivalent to adding the square
    # of the weights to the loss with plain (non-momentum) SGD.
    if self._do_use_weight_decay(param_name):
      update += self.weight_decay_rate * param

    update_with_lr = self.learning_rate * update

    next_param = param - update_with_lr

    assignments.extend(
        [param.assign(next_param),
          m.assign(next_m),
          v.assign(next_v)])
  return tf.group(*assignments, name=name)

tensorflow v1 加入了修正, 但是后续的tf2就是很混乱找不到了.

AdamWOptimizer = tf.contrib.opt.extend_with_decoupled_weight_decay(tf.train.AdamOptimizer)
optimizer = AdamWOptimizer(weight_decay=weight_decay, learning_rate=deep_learning_rate)

参考资料