深度强化学习DQN和Natural DQN, Double DQN, Dueling DoubleQN, Rainbow DQN 的演变和必看论文.

DQN的Overestimate

DQN 基于 Q-learning, Q-Learning 中有 Qmax, Qmax 会导致 Q现实 当中的过估计 (overestimate). 而 Double DQN 就是用来解决过估计的. 在实际问题中, 如果你输出你的 DQN 的 Q 值, 可能就会发现, Q 值都超级大. 这就是出现了 overestimate.

DQN 的神经网络部分可以看成一个 最新的神经网络 + 老神经网络, 他们有相同的结构, 但内部的参数更新却有时差. Q现实 部分是这样的:

$$Y_t^\text{DQN} \equiv R_{t+1} + \gamma \max_a Q(S_{t+1}, a; \theta_t^-)$$

过估计 (overestimate) 是指对一系列数先求最大值再求平均，通常比先求平均再求最大值要大（或相等，数学表达为：

$$E(\max(X_1, X_2, …)) \ge \max(E(X_1), E(X_2), …)$$

一般来说Q-learning方法导致overestimation的原因归结于其更新过程，其表达为：

$$Q_{t+1} (s_t, a_t) = Q_t (s_t, a_t) + a_t(s_t, a_t)(r_t + \gamma \max a Q_t(s_{t+1}, a) - Q_t(s_t, a_t))$$

而更新最优化过程如下

$$\forall s, a: Q(s, a)=\sum_{s^{\prime}} P_{s a}^{s^{\prime}}\left(R_{s a}^{s^{\prime}}+\gamma \max _{a} Q\left(s^{\prime}, a\right)\right)$$

把N个Q值先通过取max操作之后，然后求平均(期望)，会比我们先算出N个Q值取了期望之后再max要大。这就是overestimate的原因。

一般用于加速Q-learning算法的方法有：Delayed Q-learning, Phased Q-learning, Fitted Q-iteration等

overestimation bias in experiments across different Atari game environments:

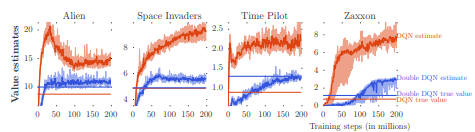
Source: “Deep Reinforcement Learning with Double Q-learning” (Hasselt et al., 2015),

traditional DQN tends to significantly overestimate action-values, leading to unstable training and low quality policy

Source: “Deep Reinforcement Learning with Double Q-learning” (Hasselt et al., 2015)

Double DQN 算法 (DDQN)

Q-learning学习其实使用单估计器(single estimate)去估计下一个状态：$\max_{a} Q_{t}\left(s_{t+1}, a\right)$ 是 $E \{ \max_{a} Q_{t}\left(s_{t+1}, a\right) \}$的一个估计。根据原理部分，Double Q-learning将使用两个estimators函数 $Q^A$和$Q^B$, 每个estimator 都会使用另一个 estimator函数的值更新下一个状态。两个函数都必须从不同的经验子集中学习，但是选择执行的动作可以同时使用两个值函数。 该算法的数据效率不低于Q学习。 在实验中作者为每个动作计算了两个Q值的平均值，然后对所得的平均Q值进行了贪婪探索。

2个estimator会导致underestimate而不会overestimate。具体证明见原文。

Double DQN学习的方式

The standard Q-learning update for the parameters after taking action At in state St and observing the immediate reward Rt+1 and resulting state St+1 is then

$$\theta_{t+1} = \theta_t + \alpha (Y^Q_t - Q(S_t, A_t; \theta_t)) \nabla_{\theta_t} Q(S_t, A_t; \theta_t).$$

where α is a scalar step size, $Y^Q_t$是一个termporal difference的值, 每次更新, one set of weights is used to determine the greedy policy and the other to determine its value.

$$Y_t^Q = R_{t+1} + \gamma Q(S_{t+1}, argmax_a Q(S_{t+1}, a; \theta_t); \theta_t).$$

使用DQN, $\theta^-$为The target network的参数, 每τ steps更新 $\theta_t^- = \theta_t$

$$Y_t^{DQN} \equiv R_{t+1} + \gamma \max_a Q(S_{t+1}, a; \theta^-_t). $$

它greedy预估下一个action时使用参数 $\theta_t$ ，同时evaluation时也采用同一套参数，让Q-learning更加容易overestimate。

因此，double Q-learning使用两个network，online network和target network，两套参数 $\theta_t, \theta_t’$ 分别进行selection和evaluation,

$$Y_t^{DoubleQ} \equiv R_{t+1} + \gamma Q(S_{t+1}, argmax_aQ(S_{t+1},a; \theta_t); \theta’_t). $$

Double DQN则是把$\theta_t’$替换为target network 的 $\theta_t^-$, 用于评估当前的greedy policy 的值, 其余和DQN基本一致. 这是DQN使用Double q-learning代价最小的方式。

$$Y_t^{DoubleDQN} \equiv R_{t+1} + \gamma Q(S_{t+1}, argmax_aQ(S_{t+1},a; \theta_t), \theta^-_t). $$

The idea of Double Q-learning is to reduce overestimations by decomposing the max operation in the target into action selection and action evaluation.

the target network in the DQN architecture provides a natural candidate for the second value function, without having to introduce additional networks.

Dueling DQN（D3QN）

Intuitively, the dueling architecture can learn which states are (or are not) valuable, without having to learn the effect of each action for each state. This is particularly useful in states where its actions do not affect the environment in any relevant way.

在某些状态场景中，动作对环境几乎没有影响，比如游戏中的等待时间，无论玩家做什么操作，对结果也没影响。而dueling架构的的目的就是解耦动作和状态。这是开车的游戏, 左边是 state value, 发红的部分证明了 state value 和前面的路线有关, 右边是 advantage, 发红的部分说明了 advantage 很在乎旁边要靠近的车子, 这时的动作会受更多 advantage 的影响. 发红的地方左右了自己车子的移动原则.

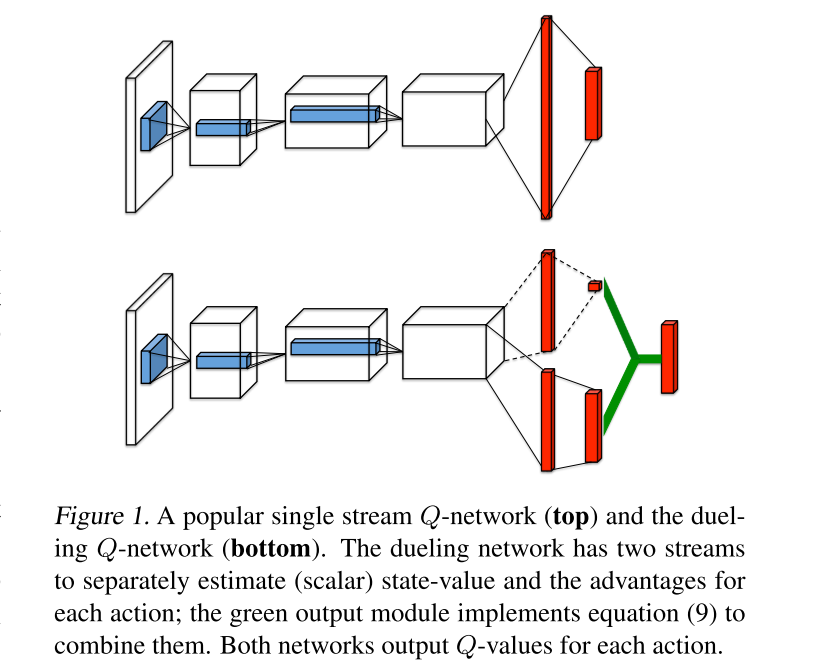
Source: “Deep Reinforcement Learning with Double Q-learning” (Hasselt et al., 2015)

Source: “Deep Reinforcement Learning with Double Q-learning” (Hasselt et al., 2015)

Dueling DQN将 state values 和 action advantages 分开，

  • state values仅仅与状态$S$有关，与具体要采用的动作$A$无关，这部分我们叫做价值函数部分，记做$V(S,w,\alpha)$, $V^{\pi}(s)=\mathbb{E}_{a \sim \pi(s)}\left[Q^{\pi}(s, a)\right]$
  • action advantages 优势函数(Advantage Function), 用于衡量 action 的相对优势, 通过让Q值减去V值得到, 记为$A(S,A,w,\beta)$, $A^\pi(s, a) = Q^\pi(s, a) - V^\pi(s)$,

价值函数 V 衡量它处于特定状态 s 的好坏程度。而Q 函数测量在此状态下选择特定操作的价值。优势函数从 Q 函数中减去状态V值，以获得每个动作重要性的相对度量。通过动作让Q和V毕竟, 最终优势函数的期望为0，即$\mathbb{E}_{a \sim \pi(s)}\left[A^{\pi}(s, a)\right] = 0$

不像DQN那样直接学出所有的Q值，Dueling DQN的思想就是独立的学出Value和Advantage，将它们以某种方式组合起来，组成Q价值函数，最直接的做法是求和：

$$Q(s, a; \theta, \alpha, \beta) = V(s; \theta,\beta) + A(s, a; \theta,\alpha)$$

其中，$w$是网络参数，而$α$是价值函数独有部分的网络参数，而$β$是优势函数独有部分的网络参数。

但是这个式子是unidentifiable, 也就是只给定Q, 我们无法还原V和A. 为了解决这个可以实现可辨识性(identifiability), 可以通过强迫优势函数的estimator在所选动作下预估其优势值为0：

$$ Q(s, a; \theta, \alpha, \beta) = V(s; \theta, \beta) + \left( A(s, a; \theta, \alpha) - \frac{1}{|A|} \sum_{a’}A(s, a’; \theta, \alpha) \right) $$

一方面这个组合方式会导致V和A丧失原先的含义, 因为它们偏离了一个常数值; 但另一方面这样可以提高优化的稳定性. 因为A的变化速度只需要和mean一样快就行, 而不是和最优的action A同步.

组合函数写进神经网络中作为输出.

Rainbow DQN

Rainbow的命名是指混合, 利用许多RL中前沿知识并进行了组合, 组合了DDQN, prioritized Replay Buffer, Dueling DQN, Multi-step learning.

Multi-step learning

原始的DQN使用的是当前的即时奖励r和下一时刻的价值估计作为目标价值，这种方法在前期策略差即网络参数偏差较大的情况下，得到的目标价值偏差也较大。因此可以通过Multi-Step Learning来解决这个问题，通过多步的reward来进行估计。

Distributional perspective RL

传统DQN中估计期望，但是期望并不能完全反映信息，毕竟还有方差，期望相同我们当然希望取方差更小的来减小波动和风险。所以从理论上来说，从分布视角（distributional perspective）来建模我们的深度强化学习模型，可以获得更多有用的信息，从而得到更好、更稳定的结果。

Noisy Net

Noisy DQN是为了增强DQN探索能力而设计的方法，是model-free，off-policy，value-based，discrete的方法。

Noisy DQN这个方法被发表在Noisy Networks for Exploration这篇文章中，但是它并不只是在DQN中被使用，实际上在A3C这样的模型中也可以增加噪声来刺激探索。

References