Java Hash Table

Hash Tables

Save items in a key-indexed table. Index is a function of the key - Hash function, method for computing array index from key.

要实现哈希表, 需要解决几个问题:

如何定义/计算哈希函数。
相等判定：如何检查两个键是否相等。
冲突解决：寻找能够处理哈希到同一索引的两个密钥的算法和数据结构。

时空权衡设计问题:

如果没有空间限制, 那么可以使用非常简单的哈希函数, 极端情况就是给每一种键分配一个索引。
如果没有时间限制, 那么对于键冲突问题可以使用简单的顺序搜索。
而现实中, 哈希表就是解决同时存在空间和时间限制的问题。

哈希函数

最理想的目标, 生成均匀分布的索引, 这样计算高效.

比如电话号码, 使用前三个数字作为索引是一种比较草稿的设计, 因为前三个数字一般代表区号, 且区号都是有限的, 这样同一个区的号码都会挤在同一个索引位置. 较好的方式是使用后三位数字. 身份证号同理.

在实际设计过程中, 不同的数据类型适用不同的方法.

所有Java类都继承了int hashCode()方法. 该方法的基本要求是: If x.equals(y), then (x.hashCode() == y.hashCode()) 最好(但不是必须的)能够满足: If !x.equals(y), then (x.hashCode() != y.hashCode()) 默认的实现方式是利用内存位置.

Java integers, booleans, and doubles:

public final class Integer
{
   private final int value;
   ...
   public int hashCode()
   {  return value;  }
}

public final class Boolean
{
   private final boolean value;
   ...
   public int hashCode()
   {
      if (value) return 1231;
      else       return 1237;
   }
}

// convert to IEEE 64-bit representation;
// xor most significant 32-bits
// with least significant 32-bits
public final class Double
{
   private final double value;
   ...
   public int hashCode()
   {
      long bits = doubleToLongBits(value);
      return (int) (bits ^ (bits >>> 32));
   }
}

strings

public final class String
{
   private int hash = 0;
   private final char[] s;
   ...
   public int hashCode()
   {
       int h = hash;
       if (h != 0) return h;
       for (int i = 0; i < length(); i++)
            hash = s[i] + (31 * h);
       hash = h;
       return h;
   }
}

Horner’s method to hash string of length L: L multiplies/adds $$h = s[0] \cdot 31^{L-1} + … + s[L-3] \cdot 31^2 + s[L–2] \cdot 31^1 + s[L–1]$$

String s = "call"; int code = s.hashCode();, $$code = 99 \cdot 31^3 + 97 \cdot 31^2 + 108 \cdot 31^1 + 108 = 3045982$$

“Standard” recipe for user-defined types. ・Combine each significant field using the 31x + y rule. ・If field is a primitive type, use wrapper type hashCode(). ・If field is null, return 0. ・If field is a reference type, use hashCode(). ・If field is an array, apply to each entry, or use Arrays.deepHashCode().

Basic rule. Need to use the whole key to compute hash code;

Modular hashing

Hash code. An int between $-2^{31}$ and $2^{31} - 1$. Hash function. An int between 0 and M - 1 (for use as array index, typically M is a prime or power of 2) A buggy version: 1-in-a-billion bug

private int hash(Key key)
{  return Math.abs(key.hashCode()) % M;  }

hashCode() of "polygenelubricants" is $-2^{31}$

A correct version

private int hash(Key key)
{  return (key.hashCode() & 0x7fffffff) % M;  }

键索引冲突

Collision. Two distinct keys hashing to same index.

Separate chaining symbol table

Use an array of M < N linked lists. (H. P. Luhn, IBM 1953)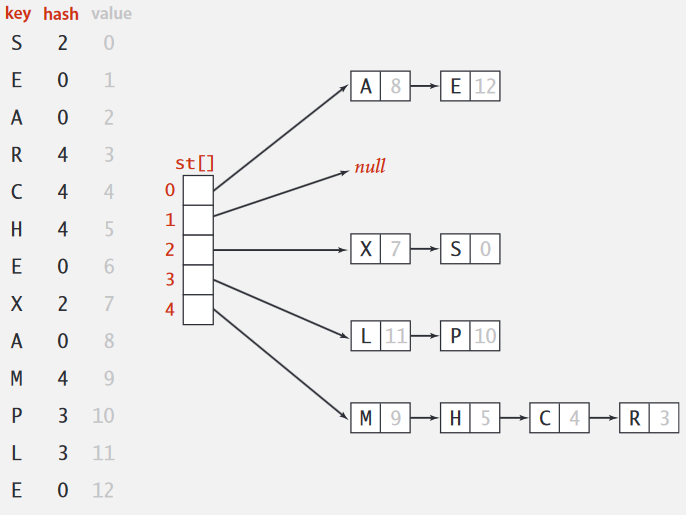

public class SeparateChainingHashST<Key, Value>
{
    private int M = 97;     // number of chains
    private Node[] st = new Node[M];  // array of chains
    private static class Node
    {
          private Object key; // no generic array creation
          private Object val;
          private Node next;
          public Node(Key key, Value val, Node next)  {
            this.key  = key;
            this.val  = val;
            this.next = next;
          }
    }

    private int hash(Key key)
    {  return (key.hashCode() & 0x7fffffff) % M;  }

    public Value get(Key key)
    {
        int i = hash(key);
        for (Node x = st[i]; x != null; x = x.next)
            if (key.equals(x.key)) return (Value) x.val;
        return null;
    }

    public void put(Key key, Value val)
    {
        int i = hash(key);
        for (Node x = st[i]; x != null; x = x.next)
          if (key.equals(x.key)) { x.val = val; return; }
        st[i] = new Node(key, val, st[i]); //new key put ahead
    }
}

Proposition. Under uniform hashing assumption, prob. that the number of keys in a list is within a constant factor of N / M is extremely close to 1. Consequence. Number of probes for search/insert is proportional to N / M

If M too large ⇒ too many empty chains.
If M too small ⇒ chains too long.
Typical choice: M ~ N / 5 ⇒ constant-time ops.

Linear Probing

Open addressing. (Amdahl-Boehme-Rocherster-Samuel, IBM 1953) When a new key collides, find next empty slot, and put it there.

Hash. Map key to integer i between 0 and M-1. Insert. Put at table index i if free; if not try i+1, i+2, etc Search. Search table index i; if occupied but no match, try i+1, i+2, etc.

public class LinearProbingHashST<Key, Value>
{
   private int M = 30001;
   private Value[] vals = (Value[]) new Object[M];
   private Key[]   keys = (Key[])   new Object[M];
   private int hash(Key key) { /* as before */  }

   public Value get(Key key)
   {
      for (int i = hash(key); keys[i] != null; i = (i+1) % M)
         if (key.equals(keys[i]))
             return vals[i];
      return null;
   }

   public void put(Key key, Value val)
   {
      int i;
      for (i = hash(key); keys[i] != null; i = (i+1) % M)
         if (keys[i].equals(key))
             break;
      keys[i] = key;
      vals[i] = val;
   }
}

Knuth’s parking problem 提供了一个理解 linear probing的模型: Cars arrive at one-way street with M parking spaces. Each desires a random space i : if space i is taken, try i + 1, i + 2, etc. So what is mean displacement of a car?

Half-full. With M / 2 cars, mean displacement is ~ 3 / 2. Full. With M cars, mean displacement is ~ sqrt(π M / 8)

Proposition. Under uniform hashing assumption, the average # of probes in a linear probing hash table of size M that contains N = α M keys is: search hit ~ (1 + 1 / (1 - α)) / 2, search miss / insert $1/2 (1 + 1 / (1 - α)^ 2)$

Typical choice: α = N / M ~ ½. So that # probes for search hit is about 3/2, # probes for search miss is about 5/2.

不同哈希表实现比较

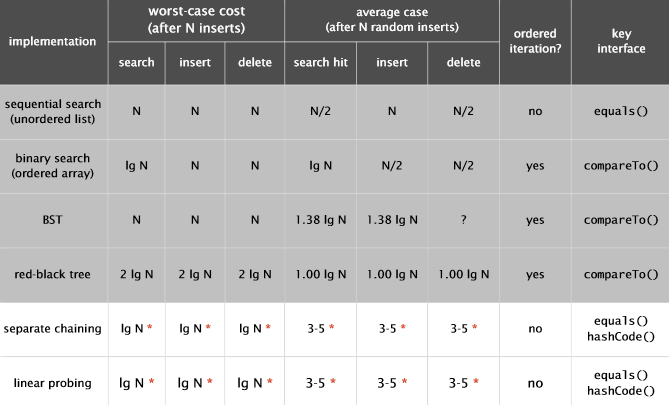Separate chaining. ・Easier to implement delete. ・Performance degrades gracefully. ・Clustering less sensitive to poorly-designed hash function.

Linear probing. ・Less wasted space. ・Better cache performance.

其他变种 Two-probe hashing. (separate-chaining variant) ・Hash to two positions, insert key in shorter of the two chains. ・Reduces expected length of the longest chain to log log N

Double hashing. (linear-probing variant) ・Use linear probing, but skip a variable amount, not just 1 each time. ・Effectively eliminates clustering. ・Can allow table to become nearly full. ・More difficult to implement delete.

Cuckoo hashing. (linear-probing variant) ・Hash key to two positions; insert key into either position; if occupied, reinsert displaced key into its alternative position (and recur). ・Constant worst case time for search.

哈希表和平衡二叉树的比较

Hash tables. ・Simpler to code. ・No effective alternative for unordered keys. ・Faster for simple keys (a few arithmetic ops versus log N compares). ・Better system support in Java for strings (e.g., cached hash code).

Balanced search trees. ・Stronger performance guarantee. ・Support for ordered ST operations. ・Easier to implement compareTo() correctly than equals() and hashCode().

Java system includes both. ・Red-black BSTs: java.util.TreeMap, java.util.TreeSet. ・Hash tables: java.util.HashMap, java.util.IdentityHashMap.

有关哈希表的攻击

均匀哈希假设在实践中是否重要？恶意攻击者学习你的哈希函数（例如，通过阅读Java API）并导致单个插槽大量堆积，从而使性能停滞不前

案例:

Bro服务器：使用比拨号调制解调器更少的带宽，将精心选择的数据包发送到DOS服务器。
Perl 5.8.0：将精心挑选的字符串插入关联数组中。
Linux 2.4.20内核：使用精心选择的名称保存文件。

单向哈希函数, 使得找到一个键对应的哈希值（或两个哈希到相同值的键）变得困难. 如已知是不安全的MD4, MD5, SHA-0和SHA-1. 其他的还有SHA-2, WHIRLPOOL, RIPEMD-160, ….

/* prints bytes as hex string */
String password = args[0];
MessageDigest sha1 = MessageDigest.getInstance("SHA1");
byte[] bytes = sha1.digest(password);

这种哈希函数对于符号表而言有点过于昂贵了

Bit Map

Bit-map用一个bit位来标记某个元素对应的Value，而Key即是该元素。由于采用了Bit为单位来存储数据，因此在存储空间方面，可以大大节省。

假设我们要对0-7内的5个元素4,7,2,5,3排序（假设这些元素没有重复）。那么我们就可以采用Bit-map的方法来达到排序的目的。要表示8个数，我们就只需要8个Bit（1Bytes），

首先我们开辟1Byte的空间，将这些空间的所有Bit位都置为0，0 0 0 0 0 0 0 0.
然后遍历这5个元素，首先第一个元素是4，那么就把4对应的位置设为1, p+(i/8)|(0x01<<(i%8)), 这里默认为Big-ending, 0 0 0 0 1 0 0 0.
然后再处理第二个元素7，将第八位置为1,，接着再处理第三个元素，一直到最后处理完所有的元素，将相应的位置为1，这时候的内存的Bit位的状态0 0 1 1 1 1 0 1
遍历一遍Bit区域，把1的索引依次输出（2，3，4，5，7），这样就达到了排序的目的。

算法的关键是如何确定十进制的数映射到二进制bit位的map图。算法占用很少内存，比如N=10000000；只需占用内存为N/8=1250000Byte=1.25M。缺点是不能有重复数据。

Map映射表

假设需要排序或者查找的总数N=10000000，那么我们需要申请内存空间的大小为int a[1 + N/32]，其中：a[0]在内存中占32位, 可以对应十进制数0-31，依次类推： bitmap表为：

a[0]--------->0-31
a[1]--------->32-63
a[2]--------->64-95
a[3]--------->96-127
..........

十进制数需要转换为对应的bit位

位移转换

将十进制数转换为对应的bit位, 申请一个int一维数组，作为32列的二维数组，

int a[0]    |0000000000000000000000000000000000000|

int a[1]    |0000000000000000000000000000000000000|

………………

int a[N]    |0000000000000000000000000000000000000|

例如十进制0，对应在a[0]第一位： 00000000000000000000000000000001

求十进制0-N对应在数组a的索引：十进制0-31，对应a[0]，先由十进制数n转换为与32的余可转化为对应在数组a中的索引0。比如n=24,那么 n/32=0，则24对应a[0]。又比如n=60, 那么n/32=1，则60对应a[1]。
求0-N对应0-31中的数：十进制0-31就对应0-31，而32-63则对应也是0-31，即给定一个数n可以通过模32求得对应0-31中的数。
利用移位0-31使得对应32bit位为1. 找到对应0-31的数为M, 左移M位：即2 ^ M, 置1.

Bloom Filter

为了降低键值冲突的概率，Bloom Filter使用了多个哈希函数：创建一个m位BitSet，先将所有位初始化为0，然后选择k个不同的哈希函数。第i个哈希函数对字符串str哈希的结果记为h(i, str)，且h(i, str)的范围是0到m-1 。

对于字符串str，分别计算h(1, str), h(2, str), ... h(k, str), 以这些哈希值作为索引, 将BitSet的对应位置的位设为1, 这样就把str映射到BitSet的k个二进制位了.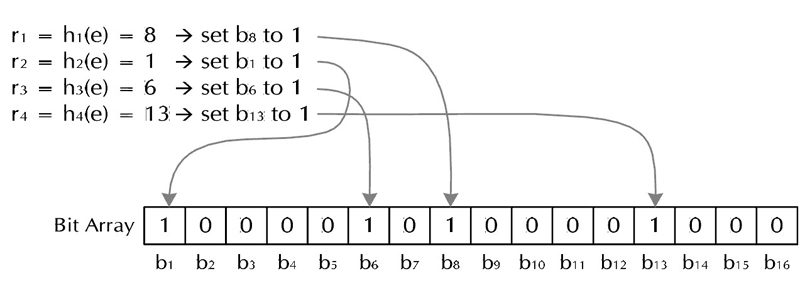

如果要检查某string是否已经被记录在BitSet中, 只需要计算其哈希值数组, 并检查BitSet上对应位置的值是否为1, 若对应位置中有任何一个不是1, 那么该字符串一定没有被记录过, 若全部对应位置都为1, 那么按照false positive认为该字符串已经被记录过了(但不是100%肯定).

删除操作会影响到其他字符串。如果需要删除字符串的功能，使用Counting bloomfilter(CBF)，这是一种Bloom Filter的变体，CBF将Bloom Filter每一个Bit改为一个计数器，这样就可以实现删除字符串的功能了。

Bloom Filter跟单哈希函数Bit-Map不同之处在于：Bloom Filter使用了k个哈希函数，每个字符串跟k个bit对应。从而降低了冲突的概率。

Hash Tables#

哈希函数#

Modular hashing#

键索引冲突#

Separate chaining symbol table#

Linear Probing#

不同哈希表实现比较#

哈希表和平衡二叉树的比较#

有关哈希表的攻击#

Bit Map#

Map映射表#

位移转换#

Bloom Filter#