本篇介绍 topic modeling, 以及一个经典的算法Latent Dirichlet allocation, 文本挖掘与语义理解的集大成者(至少在深度学习统治之前). 当然LDA不仅仅局限于文本, 还可应用于涉及大量数据集的各种问题，包括协同过滤，基于内容的图像检索和生物信息学等领域的数据。

Topic Modelling

大规模文本挖掘的核心问题, 就是用数学模型代替人力来理解文本语义，目标是找到对集合成员（如一堆文本）的数学/统计描述，以便能够对这些大型集合进行高效处理，同时保留对基本任务（如分类，检测，摘要以及相似性和相关性判断）有用的基本统计关系。

在这方面的研究方法很多，特别是信息检索(IR)领域. 一个基本方法是将语料库中的每个文档向量化，向量中的每个实数代表计数率。比如经典的tf-idf方法，用Document-Term Matrix来表达不同词在不同文档出现的情况差异, 一般term就是word作为features, 所以在这里我们表示document-word matrix(DWM), 就是DWM[i][j] = The number of occurrences of word_j in document_i. Doc 1: I have a fluffy cat. Doc 2: I see a fluffy dog.

DWM I have a fluffy cat see dog
doc1 1 1 1 1 1 0 0
doc2 1 0 1 1 0 1 1

然后进行normalization, 去和 inverse document frequency count(IDF)进行比较. IDF统计每个词在整个文档集合中出现的总次数, 通常转化为log scale, 并进行适当的normalization.

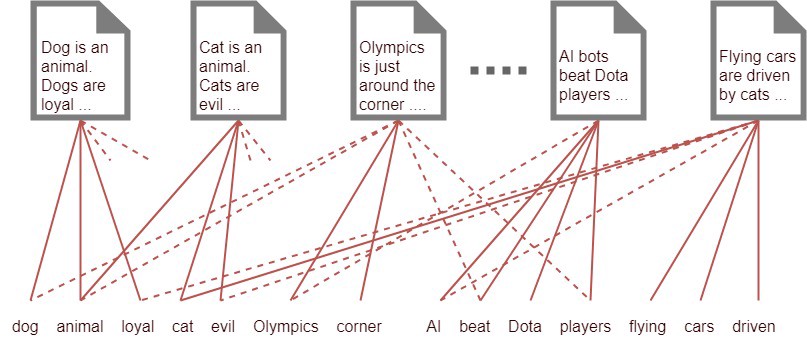
这个矩阵把文档表示为向量，使得不同文档之间可以从几何上衡量相似性，根据相似性聚类文本.

虽然tf-idf有很多很好的特性, 但是它的降维程度非常有限, 而且无法揭示文档间或文档内的统计结构.

比如我们需要知道文本包含什么信息, 却又不清楚什么信息是重要的, 所以我们希望能把信息也归纳成几类。我们称这种信息为主题, 一种粗粒度的信息. 那么就有了一个很重要的任务, 就是挖掘出这一堆文本包含的主题都有哪几大类. 每个文本都可能包含多种不同主题, 而且包含的侧重也不一样, 所以进一步的, 我们希望能够挖掘出每个文本的主题分布, 也就是主题类别在各个文本中的权重. 这种对文本信息的挖掘和理解方法, 称之为主题建模(Topic Modelling). 其核心思想是认为词不是由文档直接生成，而是由文档先生成主题，主题再生成词。

因为主题建模不再是用词频来表达, 而是用主题权重{Topic_i: weight(Topic_i, T) for Topic_i in Topics}来表达文档在K个主题上的分布。用K维的向量来表征文档，本质上是降维。

此时主题数量就是一个超参数, 通过主题建模，构建了单词的clusters而不是文本的clusters。因此，文本被表达为多个主题的混合，每个主题都有一定的权重。这种做法在机器学习的框架中可称之为隐变量模型，因为它引入了一个观测数据中不存在的变量，也就是主题这个变量。它首先假设存在这样一个隐变量，并假设了隐变量和观测变量之间的关系，然后通过模型训练得到隐变量和观测变量之间的具体关系，最终模型的产出包括隐变量的分布本身，以及更重要的，隐变量和观测变量之间的关系。

主题建模也可以理解为文本主题的tagging任务, 只是无监督罢了.

Latent Semantic Analysis (LSA)

通过引入Latent的概念，把主题表达为隐藏的信息, 也就是假设主题已经存在, 只是我们看不到. LSA使用DWM矩阵的SVD奇异值分解来确定tf-idf特征空间中的线性子空间，该子空间捕获了集合中的大部分variance。

  1. 假设单词使用中存在一些latent的结构, 由于单词选择的多样性而被掩盖了.
  2. 与其将文本表示为单词的t维空间中的向量，不如将相似词有效地组合在一起的"概念"(topic), 作为维度, 将文本（以及词本身）表示为低维空间中的向量. 这些低维的轴就是通过PCA得出的Principal Components
  3. 然后就可以在 latent semantic 空间中为下游任务服务, 如计算文本相似度(通过内积等cosine相似度计算).

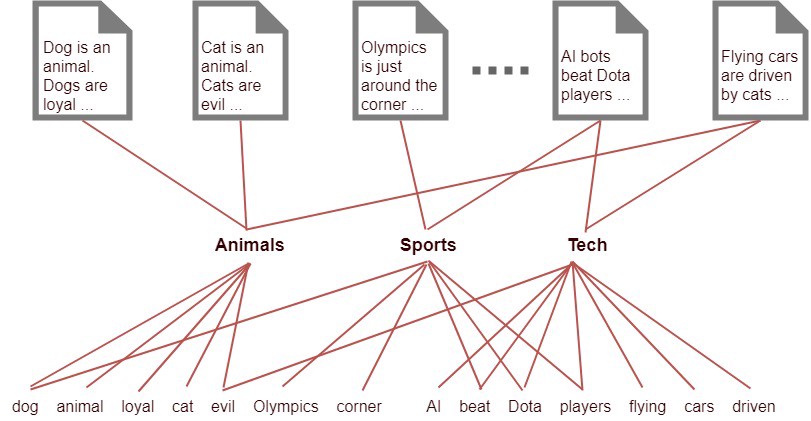
把DWM矩阵表达为 DTM(Document Topic Matrix) 和 TWM(Topic Word Matrix) 两个矩阵, 它们维度更小，相乘的结果应该尽可能近似原始的DWM矩阵。

假设词汇$V$有$1024$个, 文档$W$有$64$篇, 用 $DWM = W \times V$来表达Document-Word Matrix, 需要$64 \times 1024 = 65,536$的参数量. 假如我们设定topic参数为$8$, 那么就可以用$DWM = DTM \times TWM $来近似表达Document-Term Matrix, 参数量减少为$64 \times 8 + 8 \times 1024 = 8,704$, 缩减了将近$90%$

所以LSA核心思想是构造 Document-Term Matrix 的低阶近似.

  1. 用 tf-idf 计算加权DWM. tf-idf(term frequency–inverse document frequency)是DWM矩阵的一种经典加权表达。
  2. 然后对DWM矩阵进行 Singular Value Decomposition (SVD).

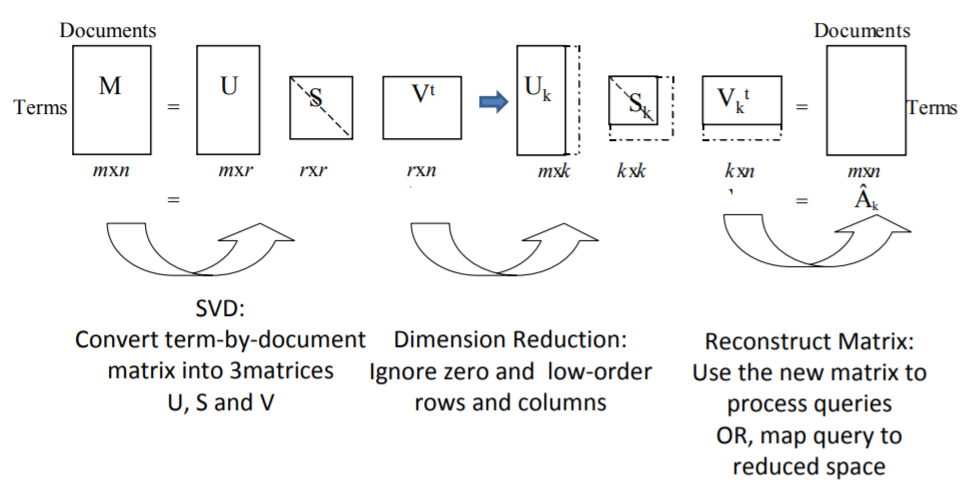
降维的意义不仅仅是减少下游任务的计算负担：

  1. tf-idf向量一般很长很庞大。因此降维操作对于聚类或分类等进一步计算是能节省很多资源。
  2. 原始DTM矩阵被认为是有噪声的：近似矩阵被解释为去噪矩阵（比原始矩阵更好的矩阵）。
  3. 假定原始的DTM矩阵相对于“真实的”DTM矩阵过于稀疏，降维也可以看作一种泛化。也就是说，原始矩阵仅列出每个文档中实际的单词，而我们可能会对与每个文档相关的所有单词感兴趣-如同义词等。

(car), (truck), (flower)} --> {(1.3452 * car + 0.2828 * truck), (flower)}

Probabilistic Latent Semantic Analysis (PLSA)

也称之为aspect model, 尝试从统计学的角度改进LSA. 将文档中的每个单词建模为混合模型中的样本. 其中这个混合模型混合的成分是multinomial随机变量，可以视为“主题”的表示形式。因此，每个单词都是由单个主题生成的，每一个文档中的不同单词可能从不同的主题生成。每个文档都表示为这些混合成分根据不同比例混合的列表，从而简化为固定主题集的概率分布.

把潜在的topics视作 Latent variable 隐变量z, 而文本Documents和词汇Words就是观察变量 observed variables. 共现(co‐occurrence)的数据都关联有隐含的话题类别, 做出条件独立假设, D和W是基于隐变量z的条件独立变量, $$ P(w|d) = \sum_{z\in Z} P(w|z)P(z|d)$$

$$ P(d, w) = P(d)P(w|d) = P(d) \sum_{z\in Z} P(w|z)P(z|d) \\ = \sum_{z\in Z} P(d) P(w|z)P(z|d) \\ = \sum_{z\in Z} P(z) P(w|z)P(d|z) $$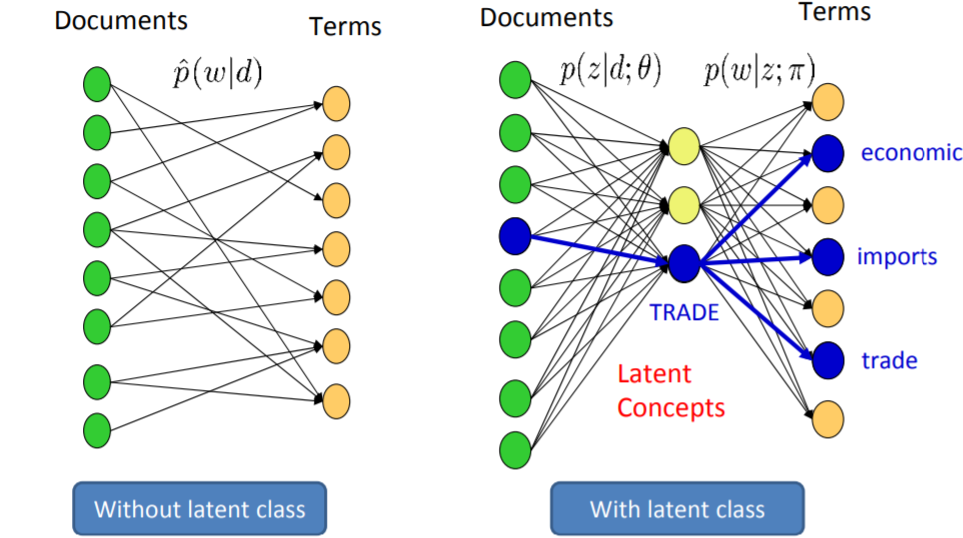

利用隐变量可以解决稀疏性问题，也就是避免文档中未出现的word的概率为零, 可以理解为一种平滑.

使用EM算法: E-Step: 计算隐变量的posterior probabilities,

  • $P(z|d, w) = \frac{ P(z) P(w|z)P(d|z) }{ \sum_{z’\in Z} P(z’) P(w|z’)P(d|z’) }$

M-Step: 更新参数

  • $P(w|z) \propto \sum_{d \in D} n(d, w) P(z|d, w) $
  • $P(d|z) \propto \sum_{w \in W} n(d, w) P(z|d, w) $
  • $P(z) \propto \sum_{d \in D}\sum_{w \in W} n(d, w) P(z|d, w) $

PLSA是一种生成式的概率模型. PLSA的$P(w, d)$可以解释为LSA中的$P = U Σ V^T$, 其中$U$包含$P(d|z)$, $Σ$作为$P(z)$的对角矩阵, $V$包含$P(w|z)$

PLSA有助于处理多义词(Polysemous words), 通过$P(w|z)$排序比较, 比如SEGMENT在topic1中更靠近image, 意味着Image region; 在topic2中更靠近sound, 意味着Phonetic segment.

虽然PPCA也是概率模型, 但是PPCA假设了正态分布(normal distribution), 局限性很大. PLSA将每个共现的概率建模为条件独立的多项式分布(multinomial distributions)的混合. 多项式分布在此领域是更好的选择。

因为有了$p(z|d)$充当特定文档的主题混合权重, pLSA可以捕获文档包含多个主题的可能性. 但是, $d$是训练集文档列表的虚拟索引, 因此$d$是一个多项式随机变量，其值可能与训练文档一样多, 这样pLSA仅针对训练集的文档学习主题混合$p(z|d)$, 对于训练集之外的document而言, 不知道如何分配概率. 等于说pLSA并不是一个定义明确的文档级别的概率生成模型。

除此之外, 因为使用训练集文档索引的分布，另一个困难就是需要估计的参数数量随着训练集数量增加而线性增加. 具体地说, 一个k-topic pLSA的参数是$k$个latent topic上大小为$V$的多项式分布, 以及$M$个mixtures, 参数量是$kV + kM$，随着$M$线性增长。所以pLSA容易过拟合(虽然可以用Tempered EM算法来稍微缓解).

Latent Dirichlet allocation(LDA)

回顾LSA和pLSA, 都基于“词袋”的假设。从概率论的角度来说，是对文档中单词有exchangeability的假设（Aldous，1985）。此外，尽管很少正式地陈述这些方法，但这些方法还假定文档是可交换的。语料库中文档的特定顺序也可以忽略。Finetti（1990）提出的经典表示定理认为任何可交换随机变量的集合都具有表示为混合分布的形式 - 通常是无限混合。因此，如果我们希望考虑文档和单词的可交换表示形式，则需要考虑能够同时捕获单词和文档的可交换性的混合模型。这就是Latent Dirichlet allocation. David Blei, Andrew Ng, and Michael Jordan. 2003.这篇文章的动机.

LDA对主题分布的基本设定是, 每个文档被表达为latent variables(topics)的随机混合, 其中各个topics可以由单词的概率分布来描述.

对于语料库$D$中的每个文档$\mathbb{w}$, LDA假设如下的生成过程:

  1. 选择参数$N ∼ Poisson(ξ)$,
  2. 用Dirichlet分布$Dir(\alpha)$生成一个多项式分布参数$θ$, 即$p(θ|\alpha)$
  3. 对于文档中的每一个词$w_n$:
    1. 基于多项式概率分布$Multinomial(θ)$选择一个topic$z_n$, 即$p(z_n |θ)$
    2. 基于$p(w_n | z_n, β)$, 即以topic $z_n$为条件的multinomial概率, 选择一个词$w_n$

这个过程做了几个假设. 一个是, $\beta$作为单词概率的参数, 是一个$k \times V$的矩阵, $\beta_{ij} = p(w^j = 1 | z^i = 1)$, 是需要估计的固定变量. 这里要注意，$N$是独立于所有其他数据生成变量（$θ$和$z$）, 因此是一个辅助变量，通常会忽略它的随机性。其余的假设有兴趣可以去读论文.

给定了参数$\alpha$和$\beta$, 可以估计topic mixture θ，一组$N$个主题$\mathbb{z}$和一组$N$个单词$\mathbb{w}$的联合分布: $$ p(θ,\mathbb{z}, \mathbb{w}|α,β) = p(θ|α) \prod^N_{n=1} p(z_n | \theta) p(w_n|z_n, \beta) $$

$p(z_n |θ)$在这里就是第$i$个$\theta_i$, 这个独特的$i$使得$z^i_n = 1$. 沿着$θ$求积分并在$z$上求和，得到文档的 marginal distribution $$p(\mathbb{w}|α,β) = \int p(θ|α) \Bigg( \prod\limits^N_{n=1} \sum\limits_{z_n} p(z_n | \theta) p(w_n|z_n, \beta) \Bigg) d\theta$$

最后，取各个文档的marginal distribution的乘积，得到整个语料库(corpus)的概率 $$ p(D|α,β) = \prod\limits^M_{d=1} p(\mathbb{w}|α,β) $$

参数$\alpha$和$\beta$是语料库级别的参数，假定在生成语料库的过程中只采样一次。$\theta_d$是文档级别的变量, 每个文档采样一次. $z_{dn}$和$w_{dn}$是词级别的变量, 每个文档的每个词采样一次.

LDA通过将主题混合权重视为k-parameter隐随机变量，而不是与训练集显式关联的一大套参数, 解决pLSA的缺陷。而且k-topic的LDA模型参数量是$k + kV$, 不会随着训练语料库的增加而增长.

如果在几何上比较和理解pLSA和LDA, 模型都可以视为在words的分布空间上操作, 每个这样的分布都可以看作(V-1)-simplex(称之为word simplex)上的一个点. 如图, 假设有3个单词, 假设选择k=3的topic simplex包含在三个单词的word simplex中。word simplex的三个角对应于三个特殊的分布([1, 0, 0], [0, 1, 0], [0, 0, 1])，即其中各有一个单词的概率为1。topic simplex的三个点对应于三个不同的单词分布(比如类似[0.7, 0.2, 0.1], [0.05, 0.9, 0.05], [0.3, 0.05, 0.65])。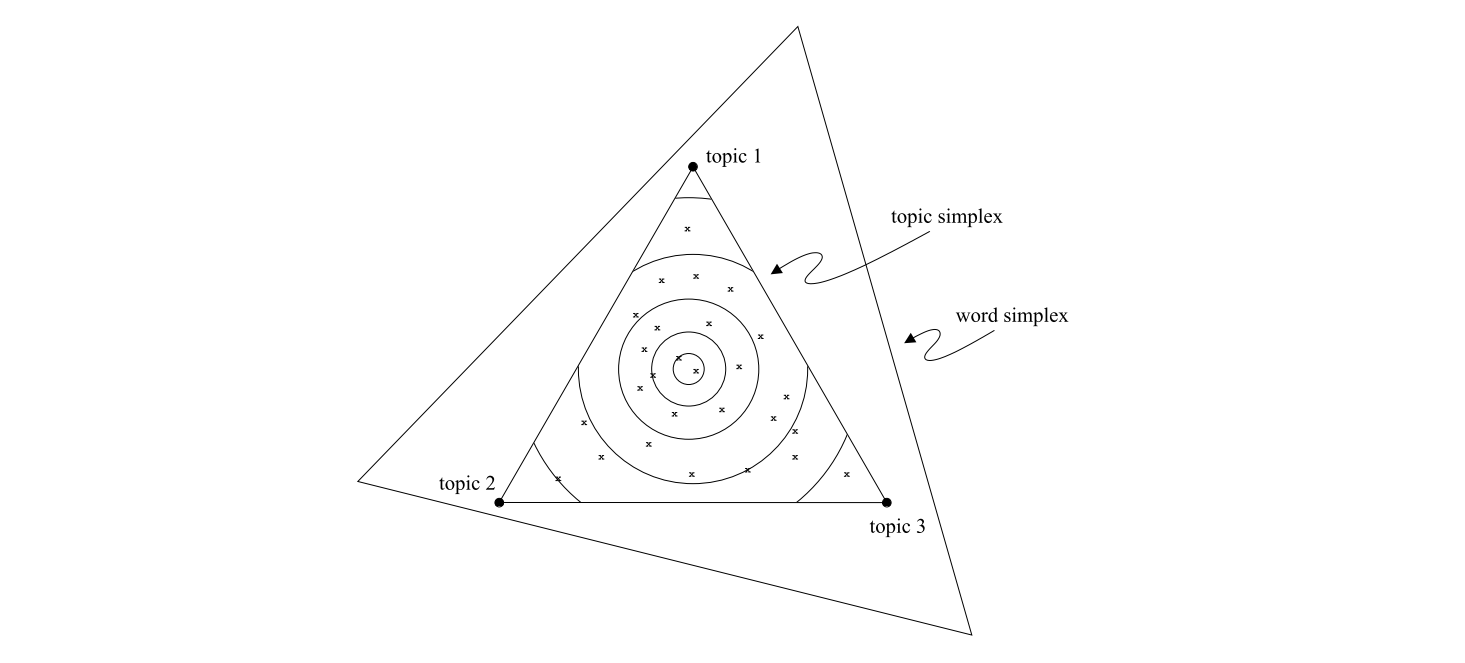

最简单的unigram模型在word simplex上找到一个点，并假设语料库中的所有单词都来自相应的分布。而隐变量模型考虑(选择)word simplex上的k个点(在图中是k=3个)，并基于这些点形成sub-simplex，即topic simplex。

  • pLSA模型假定训练集文档的每个单词各来自一个随机选择的主题。主题本身来自document-specific的主题分布，即topic simplex上的一个个点x。每个文档都有一个这样的分布；因此，文档训练集定义了关于topic simplex的经验分布。
  • LDA假定，不管是训练集还是测试集的文档, 每个单词都是由随机选择的主题生成的，该主题是从一个以随机选择的$θ_d$为参数的分布中得出的。参数$θ_d$的采样方法是每个文档采样一个topic simplex的平滑分布, 就是图中的等高线。

LDA推理和参数估计

LDA推理关键的一步是计算给定的一个文档的隐变量的后验分布(posterior distribution): $$ p(θ, \mathbb{z} | \mathbb{w}, α, β) = \frac{p(θ, \mathbb{z}, \mathbb{w} | α, β)}{p( \mathbb{w} | α, β)} $$

其中的$p(\mathbb{w}|α,β)$由于latent topics的求和中$θ$和$β$之间的耦合而变得很难求解(Dickey, 1983). 尽管因为后验分布导致精确的推理是很难，但对于LDA，可以考虑使用各种近似算法，包括Laplace逼近，变分(variational)逼近和Markov chain Monte Carlo(Jordan, 1999)。

论文中介绍了一种convexity-based variational inference方法, 基本思想是利用Jensen’s inequality获得log likelihood的可调下限(Jordan, et al., 1999)

使用迭代逼近来计算DLA模型：

  1. 初始化：每个单词随机分配给一个主题。
  2. 循环遍历每个单词，基于以下信息将单词重新分配给一个主题：
  • training: repeat until converge
    1. assign each word in each document to one of T topics.
    2. For each document d, go through each word w in d and for each topic t, compute: p(t|d), P(w|t)
    3. Reassign w to a new topic, where we choose topic t with probability P(w|t)xP(t|d)

LDA的实际应用

LDA聚类的结果经常被用来做聚类，典型的如文档的聚类，而其他表征学习学到的ID表征，同样可以用来做ID的聚类，例如用词向量做词的聚类等。能生成向量表示，并且能用来聚类，从这个角度来看，表征学习和LDA这类生成式模型的用途是一样。

以LDA为代表的生成式模型，或者叫生成式表征学习方法的应用面也非常的广，只要我们能把问题抽象成“文档+词”这样的结构，LDA几乎都可以给出一个有效的表示，例如“用户和群组”、“用户和POI”、“用户和商品”等关系都可以解构为“文档和词”这样的关系，从而可使用LDA模型计算主题和表征。此外，即使是在word2vec及其通用方法横空出世之后，LDA类方法应用仍然非常广泛。

LDA模型实战案例

总结

主题建模的算法:

  1. (p)LSA: (Probabilistic) Latent Semantic Analysis – Uses Singular Value Decomposition (SVD) on the Document-Term Matrix. Based on Linear Algebra. SVD假设了Gaussian distributed.
  2. LDA: latent Dirichlet allocation, 假设了multinomial distribution。

LDA是pLSA的generalization, LDA的hyperparameter设为特定值的时候，就specialize成 pLSA 了。从工程应用价值的角度看，这个数学方法的generalization，允许我们用一个训练好的模型解释任何一段文本中的语义。而pLSA只能理解训练文本中的语义。（虽然也有ad hoc的方法让pLSA理解新文本的语义，但是大都效率低，并且并不符合pLSA的数学定义。）这就让继续研究pLSA价值不明显了。

  1. NMF – Non-Negative Matrix Factorization
  2. Generalized matrix decomposition 实际上是 collaborative filtering 的 generalization，是用户行为分析和文本语义理解的共同基础.

参考资料