What is Word Lattices?
A word lattice is a directed acyclic graph with a single start point and edges labeled with a word and weight. Unlike confusion networks which additionally impose the requirement that every path must pass through every node, word lattices can represent any finite set of strings (although this generality makes word lattices slightly less space-efficient than confusion networks)

语音识别结果的最优路径不一定与实际字序列匹配,所以人们一般希望能够得到得分最靠前的k-best条候选路径。为了紧凑地保存候选路径,防止占用过多内存空间,可以采用词格(Word Lattice)来保存识别的候选序列。
在序列标注任务中,一般的编码器+CRF的分词模型,因为实体标签的定义不同,词汇不同,语料不同等等原因,普遍无法适应垂直领域的问题。如果要适配,需要走一遍数据准备和模型训练验证的流程。
所以实践中一般都需要词典来匹配。词典匹配方法直接针对文本进行匹配从而获得成分识别候选集合,再基于词频(基于各种工程经验统计获得)筛选输出最终结果。这种策略比较简陋,对词库准确度和覆盖度要求极高,所以存在以下几个问题:
- 未登录词,易引起切分错误
- 粒度不可控
- 节点权重如何设定, 比如
每夜总会加班涉及每夜和夜总会
因此我们需要把词典匹配方法和神经网络NER模型结合使用. 需要结合CRF模型的实体(term-标签)和基于领域字典匹配的Term(可以加上pos标签),求解文本的分词+NER划分的最优解。最优解的评判标准就是概率模型, 如果把一句话当作各个term序列, 那么文本序列标签最优解就是序列的最大联合概率
$$ \begin{aligned} \arg \max \prod_i P(w_i) & = \arg \max \log \prod_i P(w_i)\\\ & = \arg \max \sum_i \log P(w_i) \end{aligned} $$这里$w_i$指文本的每个term.
因为一句话中, NER模型和词典匹配的结果可能粒度不同或者互相交叉, 所以我们需要在所有组合中找出一个联合概率最大的组合.
利用分词工具的词典匹配功能
词典匹配的方法很多, 比如使用Trie树匹配. 这里为了简便直接使用Jieba分词来模拟词典匹配, 因为其底层实现也是一种词典匹配. 为了检索词典中的词,jieba一开始采取的思路是构建前缀Trie树以缩短查询时间。Jieba用了两个dict,trie dict用于保存trie树,lfreq dict用于存储词 -> 词频. 后来Pull request 187提出把前缀信息也放到lfreq, 解决纯Python中Trie空间效率低下的问题. 引用部分说明如下:
对于
get_DAG()函数来说,用Trie数据结构,特别是在Python环境,内存使用量过大。经实验,可构造一个前缀集合解决问题。该集合储存词语及其前缀,如
set(['数', '数据', '数据结', '数据结构'])。在句子中按字正向查找词语,在前缀列表中就继续查找,直到不在前缀列表中或超出句子范围。大约比原词库增加40%词条。
建模
一个句子所有的分词和实体组合构成了有向无环图(Directed Acyclic Graph, DAG)$G=(V,E)$,一个词对应与DAG中的的一条边$e \in E$,边的起点为词的初始字符,边的结点为词的结束字符。DAG可以用dict表示,key为边的起点,value为边的终点集合, 比如sentence = '微软银行收购tiktok'的DAG就是
{0: [(0, '微'), (1, '微软'), (3, '微软银行')],
1: [(1, '软'), (2, '软银')],
2: [(2, '银'), (3, '银行')],
3: [(3, '行')],
4: [(4, '收'), (5, '收购')],
5: [(5, '购')],
6: [(6, 't'), (8, 'tik'), (11, 'tiktok')],
...}
4 -> 5表示词'收购'。
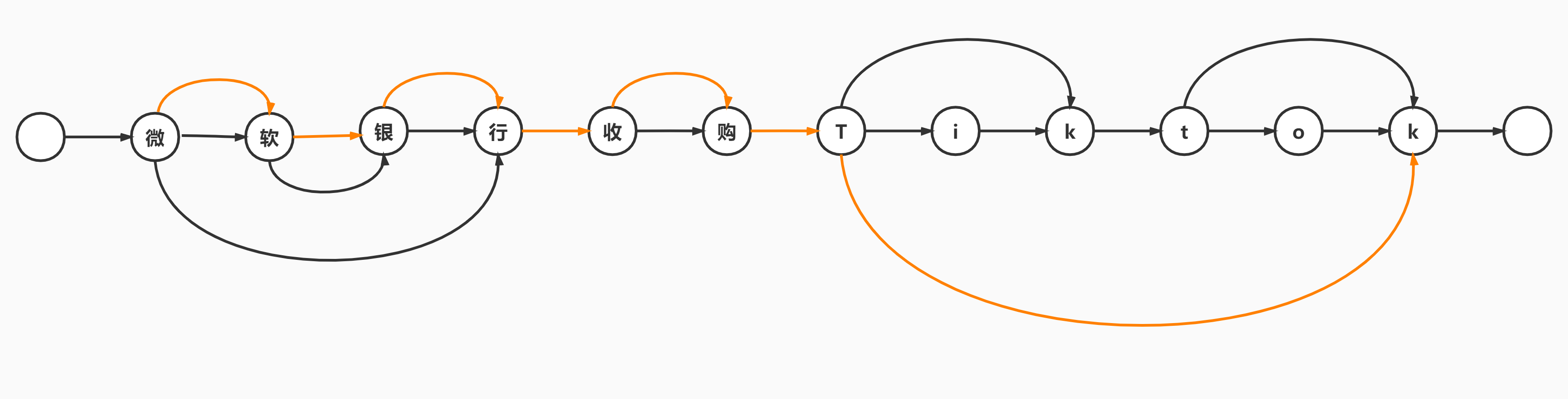
这里面有的是词, 有的是实体如'微软'等. 我们可以给它们赋予不同的权重分值, 以强化我们的输出偏好. 一般以工程统计的频率作为权重.
将词频的log值作为图$G$边的权值,将联合概率求解从连乘变为求和, 最大概率问题转换为最大分值路径问题;在上面的DAG中,节点0表示源节点,节点m-1表示尾节点;则$V=\{0, \cdots , m-1 \}$,且DAG顶点的序号的顺序与图流向是一致的:
参考jieba.get_DAG()函数,我们修改一下DAG的格式,使其包含一些我们想要的信息,比如权重等等.
def get_DAG(self, sentence):
self.check_initialized()
DAG = {}
N = len(sentence)
for k in range(N):
tmplist = []
i = k
frag = sentence[k]
while i < N and frag in self.FREQ:
if self.FREQ[frag]:
tmplist.append((i, self.get_weight(frag), 'SEG'))
i += 1
frag = sentence[k:i + 1]
if not tmplist:
tmplist.append((k, self.get_weight(frag), 'SEG'))
DAG[k] = tmplist
return DAG
get_weight可以在线的提取每个分词对应的权重
def get_weight(self, segment):
return log(self.FREQ.get(segment) or 1) - self.logtotal
这里主要是涉及到热更新词和词频的考虑, 所以每一次都从头计算一遍, 但是在分布式中这些都可以通过工程设计规避掉.
然后把NER的结果也按照类似Ditc{offest: [(end_id, weight, tag), ...]}格式加入到DAG中,就可以统一求解了。
求解概率图
图的最大路径问题其实是最短路径的对称问题. 在图论中针对DAG的最短路径求解的经典算法是按照图节点的Topological顺序, 更新从每一个节点出发的所有边. 而计算Topological顺序需要DFS遍历所有节点和边.
不过这里使用比较容易实现的动态规划方法, 直接计算最大分值路径. 如果用$d_i$表示源节点到节点$i$的最大路径的值,则有
$$d_i = \max_{(j,i) \in E} \ \{ d_j+w(j,i) \}$$其中,$w(j,i)$表示词$c_j^i$的词频log值,若$j = i$就表示字符独立成词的词频log值。
考虑到DAG是以Start -> [end0, end1, ...]的形式表达, 在定义状态时, 用$r_i$标记节点$i$到尾节点的最大路径的值, 这样可以从句子尾部往前计算, 保证考虑的每一个边不会往前越界.
根据上面设定的DAG的格式Dict{offest: [(end_id, weight, tag), ...]}, 则可以这样计算:
def calc(self, sentence, DAG, route={}):
N = len(sentence)
route[N] = (0, 0)
for idx in xrange(N - 1, -1, -1):
route[idx] = max((x[1] + route[x[0] + 1][0], x[0], x[2]) for x in DAG[idx])
return route
返回最大路径
def get_seg(self, sentence, route):
N = len(sentence)
x = 0
while x < N:
y = route[x][1] + 1
word = sentence[x:y]
yield (word, route[x][2])
x = y
return segs